
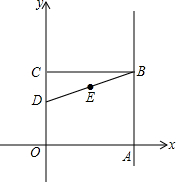
 ��ͼ��O������ԭ�㣬����OABC�Ķ���A��z����������ϣ���C��y����������ϣ���D�ڱ�OC�ϣ��ҵ�B��6��5����tan��CBD=$\frac{1}{3}$��
��ͼ��O������ԭ�㣬����OABC�Ķ���A��z����������ϣ���C��y����������ϣ���D�ڱ�OC�ϣ��ҵ�B��6��5����tan��CBD=$\frac{1}{3}$������ ��1�����ݵ�B�����꣬�ɵ�BC=6������tan��CBD=$\frac{1}{3}$�����ɽ��
��2���ٵ���PBE�ס�PEAʱ��$\frac{PA}{PE}=\frac{PE}{PB}$����PE2=PA•PB����E��FG��BC�ֱ�OC��AB��G��F���õ�GE�ǡ�BCD����λ�ߣ��Ӷ��õ�BF=CG=$\frac{1}{2}CD$=1��GE=$\frac{1}{2}BC$=3��AF=4��EF=3����PA=|t|��PB=|t-5|��PF=|t-4|�������ɹ��ɶ����ã�PE2=PF2+EF2=��t-4��2+32������PE2=PA•PB=|t��t-5��|���õ���t-4��2+32=��t��t-5�����ⷽ�̼��ɽ��
��MN��BD����ȣ��������£������ھ���OABC�У���BCO=90�㣬CD=2��BC=6�����BD=$\sqrt{{2}^{2}+{6}^{2}}=2\sqrt{10}$����ͼ2����O��OQ��MN����BC�ڵ�Q����OQ=MN=BD=2$\sqrt{10}$��CQ=$\sqrt{15}$���Ӷ�ȷ��Q��$\sqrt{15}$��5�������ֱ��OQ�ĺ�����ϵʽΪy=$\frac{\sqrt{15}}{3}$x��ֱ��MN�ĺ�����ϵʽΪy=$\frac{\sqrt{15}}{3}x$+4-$\sqrt{15}$����y=5����$\frac{\sqrt{15}}{3}x$+4-$\sqrt{15}$=5��
��ã�x=$\frac{15+\sqrt{15}}{5}$������${N}_{1}��\frac{15+\sqrt{15}}{5}��5��$���ɾ��εĶԳ��Եã�${N}_{2}��\frac{15-\sqrt{15}}{5}��5��$������CN=$\frac{15-\sqrt{15}}{5}$Ҳ�������⣮
��� �⣺��1���ߵ�B��6��5����
��BC=6��
��Rt��BCD��tan��CBD=$\frac{CD}{BC}$=$\frac{1}{3}$��
��CD=$\frac{1}{3}BC=\frac{1}{3}��6$=2��
�ʴ�Ϊ��2��
��2���٣�����PBE�ס�PEAʱ��$\frac{PA}{PE}=\frac{PE}{PB}$����PE2=PA•PB��
��ͼ1����E��FG��BC�ֱ�OC��AB��G��F��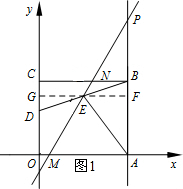
��GE�ǡ�BCD����λ�ߣ�
��BF=CG=$\frac{1}{2}CD$=1��GE=$\frac{1}{2}BC$=3
��AF=AB-BF=5-1=4��EF=GF-GE=6-3=3��
��PA=|t|��PB=|t-5|��PF=|t-4|��
��Rt��PFE�У��ɹ��ɶ����ã�PE2=PF2+EF2=��t-4��2+32��
��PE2=PA•PB=|t��t-5��|
�ࣨt-4��2+32=��t��t-5����
�ɣ�t-4��2+32=t��t-5����
��ã�t=$\frac{25}{3}$��
�ɣ�t-4��2+32=-t��t-5���ã�2t2-13t+25=0���˷���û��ʵ������
��t=$\frac{25}{3}$��
��MN��BD����ȣ��������£�
�ھ���OABC�У���BCO=90�㣬CD=2��BC=6��
��BD=$\sqrt{{2}^{2}+{6}^{2}}=2\sqrt{10}$��
��ͼ2����O��OQ��MN����BC�ڵ�Q��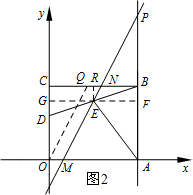
��OQ=MN=BD=2$\sqrt{10}$��
CQ=$\sqrt{O{Q}^{2}-O{C}^{2}}=\sqrt{��2\sqrt{10}��^{2}-{5}^{2}}$=$\sqrt{15}$��
��Q��$\sqrt{15}$��5����
ֱ��OQ�ĺ�����ϵʽΪy=$\frac{\sqrt{15}}{3}$x��
��ֱ��MN�ĺ�����ϵʽΪy=$\frac{\sqrt{15}}{3}$x+b����E��3��4������ã�$\frac{\sqrt{15}}{3}��3+b=4$��
��ã�b=4-$\sqrt{15}$��
��ֱ��MN�ĺ�����ϵʽΪy=$\frac{\sqrt{15}}{3}x$+4-$\sqrt{15}$��
��y=5����$\frac{\sqrt{15}}{3}x$+4-$\sqrt{15}$=5��
��ã�x=$\frac{15+\sqrt{15}}{5}$��
��${N}_{1}��\frac{15+\sqrt{15}}{5}��5��$��
�ɾ��εĶԳ��Եã�${N}_{2}��\frac{15-\sqrt{15}}{5}��5��$��
��CN=$\frac{15-\sqrt{15}}{5}$Ҳ�������⣮
��CN=$\frac{15��\sqrt{15}}{5}$��
���� �������ڼ��α任�ۺ��⣬���������������ε����ʺ��ж������ɶ�������ת�����ʡ�����ϵ���������ʽ���������Ĺؼ��Ǹ����ߵ����������ͼ���ô���ϵ������ֱ�ߵĽ���ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
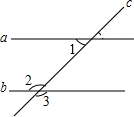 ��ͼ��a��b����3=135�㣬���1�Ķ����ǣ�������
��ͼ��a��b����3=135�㣬���1�Ķ����ǣ�������| A�� | 45�� | B�� | 55�� | C�� | 65�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
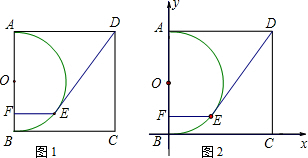
 ��ͼ������ABCD�У�O�ǶԽ���AC��BD�Ľ��㣬DE��AB��E�Ǵ��㣬DE=3��EB=1����tan��AOE=��������
��ͼ������ABCD�У�O�ǶԽ���AC��BD�Ľ��㣬DE��AB��E�Ǵ��㣬DE=3��EB=1����tan��AOE=��������| A�� | $\frac{3}{2}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
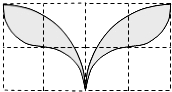 ��ͼ��С�����DZ߳�Ϊ�������Σ����Ը��ΪԲ�ģ��뾶Ϊ��2�����ֻ�Χ�ɵġ�Ҷ״����Ӱͼ�������Ϊ��������
��ͼ��С�����DZ߳�Ϊ�������Σ����Ը��ΪԲ�ģ��뾶Ϊ��2�����ֻ�Χ�ɵġ�Ҷ״����Ӱͼ�������Ϊ��������| A�� | 4��-2 | B�� | 2��-2 | C�� | 4��-4 | D�� | 2��-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
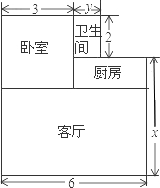 �������һ��ѧλ�����������������ϵ�ש������ṹ��ͼ��ʾ��
�������һ��ѧλ�����������������ϵ�ש������ṹ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A�� | x��y���DZ�������x���Ա�����y������� | |
| B�� | ������������Ϊ4kgʱ�����ɳ���Ϊ12cm | |
| C�� | ���ɲ�������ʱ�ij���Ϊ0cm | |
| D�� | ��������ÿ����1kg�����ɳ���y����0.5cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��5�� | B�� | 5��3�� | C�� | 5��5�� | D�� | 3��3�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com