
【题目】如图,在平面直角坐标系中,A (8,0) ,B (0,6),动点M从点A出发沿AO以每秒2个单位长度的速度向原点O运动,同时动点N从点B出发沿折线BO﹣OA向终点A运动,点N在y轴上的速度是每秒3个单位长度,在x轴上的速度是每秒4个单位长度,过点M作x轴的垂线交AB于点C,连结MN、CN.设点M运动的时间为t(秒),△MCN的面积为S(平方单位).
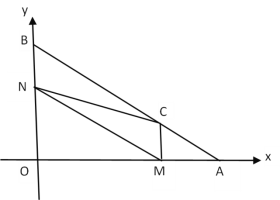
(1)当t为何值时,点M、N相遇?
(2)求△MCN的面积S(平方单位)与时间t(秒)的函数关系式;
(3)当t为何值时,△MCN是等腰三角形?
【答案】(1)![]() ;(2)当0<t≤2时,
;(2)当0<t≤2时,![]() ;当2<t<
;当2<t<![]() 时,
时,![]() ;当
;当![]() <t≤4时,
<t≤4时,![]() ;(3)当t=
;(3)当t=![]() 或
或![]() 或
或![]() 时,△MCN是等腰三角形
时,△MCN是等腰三角形
【解析】
(1)由题意列方程可求t的值;
(2)分0<t≤2,2<t<![]() ,
,![]() <t≤4三种情况讨论,由三角形的面积公式可求解;
<t≤4三种情况讨论,由三角形的面积公式可求解;
(3)分0<t≤2,2<t<![]() ,
,![]() <t≤4三种情况讨论,即可求t的值.
<t≤4三种情况讨论,即可求t的值.
解:(1)由题意可得:2t+4(t﹣2)=8
∴t=![]()
∴当t=![]() 时,点M、点N相遇;
时,点M、点N相遇;
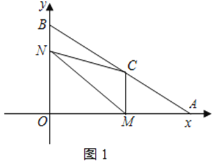
(2)∵CM⊥OA,BO⊥OA,
∴CM∥BO,
∴△CMA∽△BOA ,
∴![]() 即:
即:![]() ,
,
①如图1所示:当0<t≤2时, ![]() ,
,
②如图2所示:当2<t<![]() 时,
时,![]() ,
,
③如图3所示:当![]() ;
;
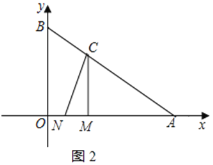
(3)应分三种情况讨论:
①当0<t≤2时,点N在BO上.
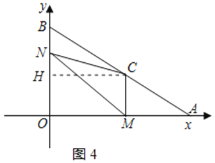
(i)如图4,过C作CH⊥OB于H,
则CH=OM=![]()
又∵CM=![]()
∴CH—CM=![]() —
—![]() =
=![]()
当0<t≤2时,![]() >0,即CH>CM
>0,即CH>CM
又CN≥CH,MN≥CH
∴CN>CM,MN>CM
即CN![]() CM,MN
CM,MN![]() MC
MC
(ii)若NC=NM时,则△MCN是等腰三角形.
此时点N在CM的垂直平分线上,
∴ON=![]() ,
,
则有:6﹣3t=![]()
解得:t=![]()
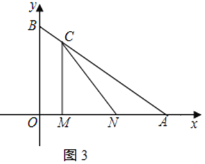
②当2<t<![]() 时,如图2所示:此时点N在OA上,且点N在点M左侧.
时,如图2所示:此时点N在OA上,且点N在点M左侧.
∵∠CMN=90°
∴只有当MC=MN时,△MCN是等腰三角形.
此时![]() ,
,
则有:![]()
解得:t=![]()
③当![]() <t≤4时,如图3所示:点N在OA上,且点N在点M右侧.
<t≤4时,如图3所示:点N在OA上,且点N在点M右侧.
同理可得:只有当MC=MN时,△MCN是等腰三角形.
此时![]()
则有:![]()
解得:t=![]()
综上所述:当t=![]() 或
或![]() 或
或![]() 时,△MCN是等腰三角形.
时,△MCN是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,点D的坐标是(0,![]() ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
(1)求A、B、C三点的坐标;
(2)求过A、B、C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
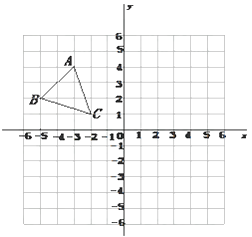
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量y(万件)与月份x(月)的关系为:![]() ,每件产品的利润z(元)与月份x(月)的关系如下表:
,每件产品的利润z(元)与月份x(月)的关系如下表:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
z | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
(1)请你根据表格求出每件产品利润z(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第九卷《勾股》章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门几何步而见木( )
A.300步B.315步C.400步D.415步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边![]() 沿射线
沿射线![]() 向右平移到
向右平移到![]() 的位置,连接
的位置,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() 互相平分;③四边形
互相平分;③四边形![]() 是菱形;④
是菱形;④![]() 。其中正确的个数是( )
。其中正确的个数是( )
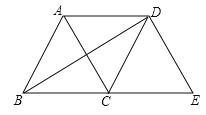
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
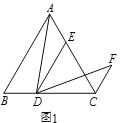
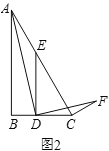
【题目】(1)问题发现:如图1,在等边![]() 中,点
中,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .则
.则![]() 与
与![]() 的数量关系是_____,
的数量关系是_____,![]() 的度数为______.
的度数为______.
(2)拓展探究:如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,当∠ADF=∠ACF=90°时,求
,当∠ADF=∠ACF=90°时,求![]() 的值.
的值.
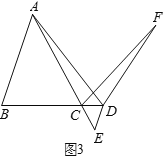
(3)解决问题:如图3,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的延长线上一点,过点
的延长线上一点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,直接写出当
,直接写出当![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数且
为常数且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 1 | 3 |
| -1 | 3 | 5 | 3 |
给出了结论:
(1)二次函数![]() 有最大值,最大值为5;(2)
有最大值,最大值为5;(2)![]() ;(3)
;(3)![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;(4)3是方程
值的增大而减小;(4)3是方程![]() 的一个根;(5)当
的一个根;(5)当![]() 时,
时,![]() .则其中正确结论的个数是( )
.则其中正确结论的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元
(1)设每件涨价x元,则每星期实际可卖出 件,每星期售出商品的利润y为 元.x的取值范围是 ;
(2)设每件降价m元,则每星期售出商品的利润w为 元;
(3)在涨价的情况下,如何定价才能使每星期售出商品的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com