
【题目】某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元
(1)设每件涨价x元,则每星期实际可卖出 件,每星期售出商品的利润y为 元.x的取值范围是 ;
(2)设每件降价m元,则每星期售出商品的利润w为 元;
(3)在涨价的情况下,如何定价才能使每星期售出商品的利润最大?最大利润是多少?
【答案】(1)(300-10x);-10x2+100x+6000;0≤x≤30;(2)-20m2+100m+6000;(3)每件定价为65元时利润最大,最大利润为6250元
【解析】
(1)根据涨价时,每涨价1元,每星期要少卖出10件,可列出销售量的代数式,根据总利润=单件利润×销售量列出函数表达式即可;
(2)根据总利润=单件利润×销售量列出函数表达式即可;
(3)根据涨价的函数表达式,利用二次函数的性质解答.
(1)∵每涨价1元,每星期要少卖出10件,
∴每星期实际可卖出(300-10x)件,
y=(60-40+x)(300-10x)=-10x2+100x+6000
∵![]() ,
,
∴0≤x≤30;
(2)设每件降价m元,则毎星期售出商品的利润w,则
W=(20-m)(300+20m)=-20m2+100m+6000,
(3)y=-10x2+100x+6000=-10(x-5)2+6250.
∴当x=5时,y有最大值,为6250,
∴在涨价的情况下,定价为60+5=65(元)
即在涨价的情况下,定价为65元时,每星期售出商品的最大利润是6250元.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A (8,0) ,B (0,6),动点M从点A出发沿AO以每秒2个单位长度的速度向原点O运动,同时动点N从点B出发沿折线BO﹣OA向终点A运动,点N在y轴上的速度是每秒3个单位长度,在x轴上的速度是每秒4个单位长度,过点M作x轴的垂线交AB于点C,连结MN、CN.设点M运动的时间为t(秒),△MCN的面积为S(平方单位).
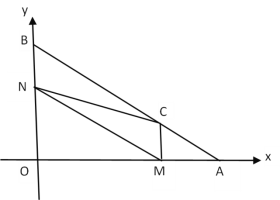
(1)当t为何值时,点M、N相遇?
(2)求△MCN的面积S(平方单位)与时间t(秒)的函数关系式;
(3)当t为何值时,△MCN是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价y1(单位:元)与它的边长x(单位:cm)满足关系式y1=![]() ,每张薄板的出厂价y2(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据.
,每张薄板的出厂价y2(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据.
薄板的边长(cm) | 20 | 30 |
出厂价(元/张) | 50 | 70 |
(1)求一张薄板的出厂价y2与边长x之间满足的函数关系式;
(2)已知:利润=出厂价﹣成本价
①求一张薄板的利润y与边长x之间满足的函数关系式;
②当边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕顶点C逆时针旋转得到△A′B′C,且点B刚好落在A′B′上.若∠A=25°,∠BCA′=45°,则∠A′BA=___________度

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,点
,点![]() 是
是![]() 轴正半轴上的动点.
轴正半轴上的动点.
(Ⅰ)当![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(Ⅱ)点![]() 在抛物线上,当
在抛物线上,当![]() ,
,![]() 时,求
时,求![]() 的值;
的值;
(Ⅲ)点![]() 在抛物线上,当
在抛物线上,当![]() 的最小值为
的最小值为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC中,AM平分∠BAC,且AM⊥BM于点M,已知AB=8,AC=20,M1、M2…Mn﹣1把线段BM分成n等份(其中n为正整数),C1、C2…C2n﹣1把线段BC分成2n等份,则M99C99=_____.
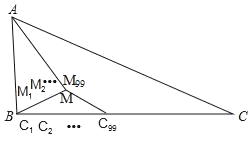
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图点O是等边![]() 内一点,
内一点,![]() ,∠ACD=∠BCO,OC=CD,
,∠ACD=∠BCO,OC=CD,
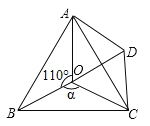
(1)试说明:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)当![]() 为多少度时,
为多少度时,![]() 是等腰三角形
是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
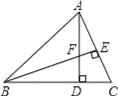
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com