【题目】如图，将△ABC绕顶点C逆时针旋转得到△A′B′C，且点B刚好落在A′B′上．若∠A＝25°，∠BCA′＝45°，则∠A′BA＝___________度
科目：初中数学 来源： 题型：
【题目】我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量y（万件）与月份x（月）的关系为：
，每件产品的利润z（元）与月份x（月）的关系如下表：
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
z | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
（1）请你根据表格求出每件产品利润z（元）与月份x（月）的关系式；
（2）若月利润w（万元）=当月销售量y（万件）×当月每件产品的利润z（元），求月利润w（万元）与月份x（月）的关系式；
（3）当x为何值时，月利润w有最大值，最大值为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数
（
，
，
为常数且
）中的
与
的部分对应值如下表：
| －1 | 0 | 1 | 3 |
| －1 | 3 | 5 | 3 |
给出了结论：
（1）二次函数有最大值，最大值为5；（2）
；（3）
时，的值随值的增大而减小；（4）3是方程
的一个根；（5）当
时，
.则其中正确结论的个数是（ ）
A.4B.3C.2D.1
查看答案和解析>>
科目：初中数学 来源： 题型：
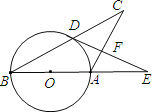
【题目】已知：如图，△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作DF⊥AC于点F，交BA的延长线于点E．求证：
（1）BD＝CD；
（2）DE是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售量
（件）与销售单价
（元）之间存在一次函数关系，如图所示.
（1）求与之间的函数关系式；
（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？
（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件；每降价1元，每星期可多卖出20件，已知商品的进价为每件40元
(1)设每件涨价x元，则每星期实际可卖出 件，每星期售出商品的利润y为 元.x的取值范围是 ；
(2)设每件降价m元，则每星期售出商品的利润w为 元；
(3)在涨价的情况下，如何定价才能使每星期售出商品的利润最大?最大利润是多少?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，
(1)求证：四边形ADCE为矩形；
(2)当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】平面直角坐标系中，直线
与x轴、y轴分别胶于A、C两点，直线
与x轴、y轴分别交于B、D两点．
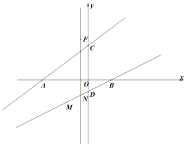
（1）如图1，点F是直线
上的动点，当
的面积等于
时，有一线段
（点M在点N的左侧）在直线BD上移动，首尾顺次连接点A、M、N、F构成四边形AMNF的周长最小时点N的横坐标．
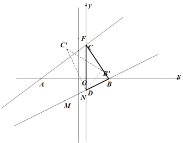
（2）如图2，将
绕点D逆时针旋转
，记旋转中的为
，若直线
与直线AC交于点P，直线与直线DC交于点Q，当
是等腰三角形时，直接写出CP的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
