
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,点
,点![]() 是
是![]() 轴正半轴上的动点.
轴正半轴上的动点.
(Ⅰ)当![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(Ⅱ)点![]() 在抛物线上,当
在抛物线上,当![]() ,
,![]() 时,求
时,求![]() 的值;
的值;
(Ⅲ)点![]() 在抛物线上,当
在抛物线上,当![]() 的最小值为
的最小值为![]() 时,求
时,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)把b=2和点![]() 代入抛物线的解析式,求出c的值,进行配方即可得出顶点坐标
代入抛物线的解析式,求出c的值,进行配方即可得出顶点坐标
(Ⅱ)根据点![]() 和)点
和)点![]() 在抛物线上和
在抛物线上和![]() 得出点
得出点![]() 在第四象限,且在抛物线对称轴
在第四象限,且在抛物线对称轴![]() 的右侧.过点
的右侧.过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,则点
,则点![]() ,再根据D、E两点坐标得出
,再根据D、E两点坐标得出![]() 为等腰直角三角形,得出
为等腰直角三角形,得出![]() ,再根据已知条件
,再根据已知条件![]() ,
,![]() ,从而求出b的值
,从而求出b的值
(Ⅲ)根据点![]() 在抛物线上得出点
在抛物线上得出点![]() 在第四象限,且在直线
在第四象限,且在直线![]() 的右侧;取点
的右侧;取点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() 与
与![]() 轴相交于点
轴相交于点![]() ,得出
,得出![]() ,此时
,此时![]() 的值最小;过点
的值最小;过点![]() 作
作![]() 轴于点
轴于点![]() ,则点
,则点![]() .再根据
.再根据![]() 得出m与b的关系,然后根据两点间的距离公式和
得出m与b的关系,然后根据两点间的距离公式和
![]() 的最小值为
的最小值为![]() ,列出关于b的方成即可
,列出关于b的方成即可
解:(Ⅰ)∵抛物线![]() 经过点
经过点![]() ,
,
∴![]() .即
.即![]() .
.
当![]() 时,
时,![]() ,
,
∴抛物线的顶点坐标为![]() .
.
(Ⅱ)由(Ⅰ)知,抛物线的解析式为![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() .
.
由![]() ,得
,得![]() ,
,![]() ,
,
∴点![]() 在第四象限,且在抛物线对称轴
在第四象限,且在抛物线对称轴![]() 的右侧.
的右侧.
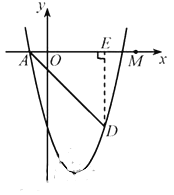
如图,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,则点
,则点![]() .
.
∴![]() ,
,![]() .得
.得![]() .
.
∴在![]() 中,
中,![]() .
.
∴![]() .
.
由已知![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
(Ⅲ)∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() .
.
可知点![]() 在第四象限,且在直线
在第四象限,且在直线![]() 的右侧.
的右侧.
考虑到![]() ,可取点
,可取点![]() ,
,
如图,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,
有![]() ,得
,得![]() ,
,
则此时点![]() 满足题意.
满足题意.
过点![]() 作
作![]() 轴于点
轴于点![]() ,则点
,则点![]() .
.
在![]() 中,可知
中,可知![]() .
.
∴![]() ,
,![]() .
.
∵点![]() ,
,
∴![]() .解得
.解得![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.


科目:初中数学 来源: 题型:
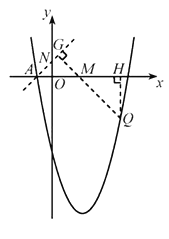
【题目】已知,在△ACB和△DCE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,M为DE的中点,联结BE.
(1)如图1,当点A、D、E在同一直线上,联结CM,求证:CM=![]() ;
;
(2)如图2,当点D在边AB上时,联结BM,求证:BM2=(![]() )2+(
)2+(![]() )2.
)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
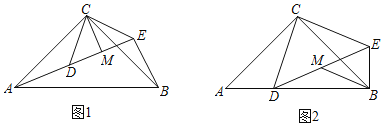
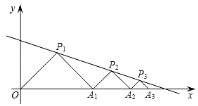
【题目】如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角顶点P1(3,3),P2,P3,…均在直线![]() 上.设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…,依据图形所反映的规律,Sn=_____.
上.设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…,依据图形所反映的规律,Sn=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:3(沿斜坡从B到D时,其升高的高度与水平前进的距离之比).已知在地面B处测得山顶A的仰角为30°,在斜坡D处测得山顶A的仰角为45°.求山顶A到地面BC的高度AC是多少米?
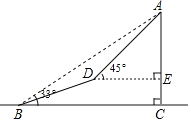
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() 的顶点A在格点上,B是小正方形边的中点,
的顶点A在格点上,B是小正方形边的中点,![]() ,
,![]() ,经过点A,B的圆的圆心在边AC上.
,经过点A,B的圆的圆心在边AC上.
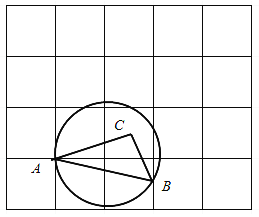
(Ⅰ)线段AB的长等于_______________;
(Ⅱ)请用无刻度的直尺,在如图所示的网格中,画出一个点P,使其满足![]() ,并简要说明点P的位置是如何找到的(不要求证明)_____.
,并简要说明点P的位置是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从沈阳到大连的火车原来的平均速度是180千米/时,经过两次提速后平均速度为217.8干米/时,这两次提速的百分率相同.
(1)求该火车每次提速的百分率;
(2)填空:若沈阳到大连的铁路长396千米,则第一次提速后从甲地到乙地所用的时间比提速前少用了 小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名射击选手中选出一名选手参加省级比赛,现对他们分别进行5次射击测试,成绩分别为(单位:环)
甲:5、6、7、9、8
乙:8、4、8、6、9
(1)分别计算这两组数据的平均数和方差;
(2)根据测试成绩,你认为选派哪一名选手参赛更好些?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在△ABC中,AB=AC.
(1)用尺规作图法在AC边上找一点D,使得BD=BC(保留作图痕迹,不要求写作法):
(2)若∠A=30°,求∠ABD的大小.
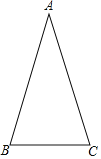
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com