
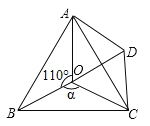
【题目】如图点O是等边![]() 内一点,
内一点,![]() ,∠ACD=∠BCO,OC=CD,
,∠ACD=∠BCO,OC=CD,
(1)试说明:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)当![]() 为多少度时,
为多少度时,![]() 是等腰三角形
是等腰三角形
【答案】(1)见解析;(2)△AOD是直角三角形,理由见解析;(3) 110°或125°或140°时,△AOD是等腰三角形.
【解析】
(1)根据CO=CD,∠OCD=60°,然后根据等边三角形的判定方法即可得到△COD是等边三角形;
(2)先求得∠ADC=∠BOC=α=150°,再利用△COD是等边三角形得∠CDO=60°,于是可计算出∠ADO=90°,由此可判断△AOD是直角三角形;
(3)先利用α表示出∠ADO=α-60°,∠AOD=190°-α,再进行分类讨论:当∠AOD=∠ADO时,△AOD是等腰三角形,即190°-α=α-60°;当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°-α)+α-60°=180°;当∠ADO=∠DAO时,△AOD是等腰三角形,即190°-α+2(α-60°)=180°,然后分别解方程求出对应的α的值即可.
(1)∵∠ACD=∠BCO
∴∠ACD+∠ACO=∠BCO+∠ACO=60°
又∵CO=CD
∴△COD是等边三角形;
(2)∵△COD是等边三角形
∴CO=CD
又∵∠ACD=∠BCO,AC=BC
∴△ACD≌△BCO(SAS)
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠CDO=60°,
∴∠ADO=∠ADC∠CDO=90°,
∴△AOD是直角三角形;
(3)∵△COD是等边三角形,
∴∠CDO=∠COD=60°,
∴∠ADO=α60°,∠AOD=360°60°110°α=190°α,
当∠AOD=∠ADO时,△AOD是等腰三角形,即190°α=α60°,解得α=125°;
当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°α)+α60°=180°,解得α=140°;
当∠ADO=∠DAO时,△AOD是等腰三角形,即190°α+2(α60°)=180°,解得α=110°,
综上所述,∠BOC的度数为110°或125°或140°时,△AOD是等腰三角形.


科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数且
为常数且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 1 | 3 |
| -1 | 3 | 5 | 3 |
给出了结论:
(1)二次函数![]() 有最大值,最大值为5;(2)
有最大值,最大值为5;(2)![]() ;(3)
;(3)![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;(4)3是方程
值的增大而减小;(4)3是方程![]() 的一个根;(5)当
的一个根;(5)当![]() 时,
时,![]() .则其中正确结论的个数是( )
.则其中正确结论的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元
(1)设每件涨价x元,则每星期实际可卖出 件,每星期售出商品的利润y为 元.x的取值范围是 ;
(2)设每件降价m元,则每星期售出商品的利润w为 元;
(3)在涨价的情况下,如何定价才能使每星期售出商品的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求画图:①仅用无刻度的直尺;②保留必要的画图痕迹.
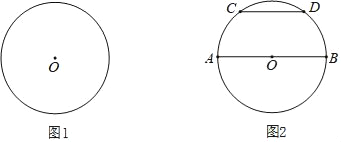
(1)如图1,画出⊙O的一个内接矩形;
(2)如图2,AB是⊙O的直径,CD是⊙O的弦,且CD∥AB,画出⊙O的一个内接正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
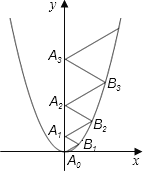
【题目】二次函数![]() 的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2008在y轴的正半轴上,点B1,B2,B3,…,B2008在二次函数
的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2008在y轴的正半轴上,点B1,B2,B3,…,B2008在二次函数![]() 位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长=__.
位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() 与x轴、y轴分别胶于A、C两点,直线
与x轴、y轴分别胶于A、C两点,直线![]() 与x轴、y轴分别交于B、D两点.
与x轴、y轴分别交于B、D两点.
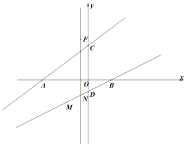
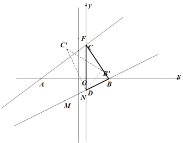
(1)如图1,点F是直线![]() 上的动点,当
上的动点,当![]() 的面积等于
的面积等于![]() 时,有一线段
时,有一线段![]() (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF的周长最小时点N的横坐标.
(点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF的周长最小时点N的横坐标.
(2)如图2,将![]() 绕点D逆时针旋转
绕点D逆时针旋转![]() ,记旋转中的
,记旋转中的![]() 为
为![]() ,若直线
,若直线![]() 与直线AC交于点P,直线
与直线AC交于点P,直线![]() 与直线DC交于点Q,当
与直线DC交于点Q,当![]() 是等腰三角形时,直接写出CP的值.
是等腰三角形时,直接写出CP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=12,点E在AD边上,且AE=8,EF⊥BE交CD于F.
(1)求证:△ABE∽△DEF;
(2)求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com