
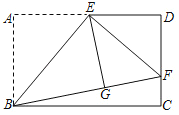
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠使点A落在点G处,延长BG交CD于点F,连接EF,若CF=1,DF=2,则BC的长是( )
A.3![]() B.
B.![]() C.5D.2
C.5D.2![]()
【答案】D
【解析】
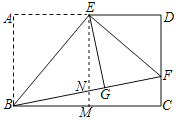
首先过点E作EM⊥BC于M,交BF于N,易证得△ENG≌△BNM(AAS),MN是△BCF的中位线,根据全等三角形的性质,即可求得GN=MN,由折叠的性质,可得BG=3,继而求得BF的值,又由勾股定理,即可求得BC的长.
解:过点E作EM⊥BC于M,交BF于N,
∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD=BC,
∵∠EMB=90°, ∴四边形ABME是矩形,
∴AE=BM, 由折叠的性质得:AE=GE,∠EGN=∠A=90°,
∴EG=BM,
∵∠ENG=∠BNM,
∴△ENG≌△BNM(AAS),
∴NG=NM,
∵E是AD的中点, ∴AE=ED=BM=CM,
∵EM∥CD,
∴BN:NF=BM:CM,
∴BN=NF,
∴NM=![]() CF=
CF=![]() ,
,
∴NG=![]() ,
,
∵BG=AB=CD=CF+DF=3,
∴BN=BG-NG=3-![]() =
=![]() ,
,
∴BF=2BN=5,
∴BC=![]()
故选:D.


科目:初中数学 来源: 题型:
【题目】无影塔位于河南汝南城南,俗传冬至正午无塔影,故称无影塔;相传为唐代和尚悟颗所建,故又称“悟颖塔”,该塔应建于北宋中、早期,为豫南地区现存最古之砖塔.某数学小组为了度量塔高进行了如下操作:用一架无人机在距离塔基![]() 8米处垂直起飞30米至点
8米处垂直起飞30米至点![]() 处,测得塔基
处,测得塔基![]() 处的俯角为
处的俯角为![]() ,将无人机沿水平方向向右飞行
,将无人机沿水平方向向右飞行![]() 米至点
米至点![]() ,在此处测得塔顶
,在此处测得塔顶![]() 的俯角为
的俯角为![]() ,请依据题中数据计算无影塔的高度.(结果精确到
,请依据题中数据计算无影塔的高度.(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某初中课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
频数 | 8 | 10 | 3 | ||
对应扇形 图中区域 | D | E | C |

(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(3)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A,B两个顶点在x轴上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,得到△A'B'C',设点B的对应点B'的横坐标为2,则点B的横坐标为( )
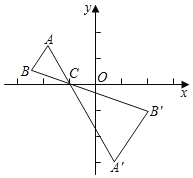
A.﹣1B.![]() C.﹣2D.
C.﹣2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点E,且点E是![]() 的中点,连接AD交BE于点F,连接EA,ED.
的中点,连接AD交BE于点F,连接EA,ED.
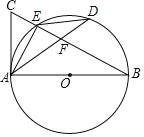
(1)求证:AC=AF;
(2)若EF=2,BF=8,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了了解2020年在疫情中上网课的感受,组织教师通过问卷和座谈等形式,随机抽取某城区一些初中学生进行调查,并将调查的普遍感受分为四大类:A.提高自律能力;B.战亲子关系;C.提升信息素养;D.教师敬业辛苦,并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
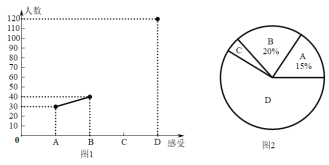
(1)此次抽样调查中,共调查了__________名初中学生;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)根据抽样调查结果,请你估计该城区1000名初中学生中有多少人的感受是“教师敬业辛苦”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 的坐标为
的坐标为![]() .点
.点![]() 是边
是边![]() 上的一个动点(不与
上的一个动点(不与![]() 、
、![]() 重合),反比例函数
重合),反比例函数![]()
![]() 的图象经过点
的图象经过点![]() 且与边
且与边![]() 交于点
交于点![]() ,连接
,连接![]() .
.
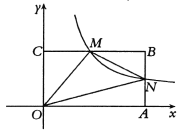
(1)当点![]() 是边
是边![]() 的中点时,求反比例函数的表达式
的中点时,求反比例函数的表达式
(2)在点![]() 的运动过程中,试证明:
的运动过程中,试证明:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
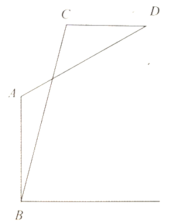
【题目】如图1,为放置在水平桌面![]() 上的台灯,底座的高
上的台灯,底座的高![]() 为
为![]() .长度均为
.长度均为![]() 的连杆
的连杆![]() ,
,![]() 与
与![]() 始终在同一水平面上.
始终在同一水平面上.
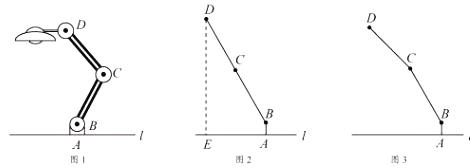
(1)旋转连杆![]() ,
,![]() ,使
,使![]() 成平角,
成平角,![]() ,如图2,求连杆端点
,如图2,求连杆端点![]() 离桌面
离桌面![]() 的高度
的高度![]() .
.
(2)将(1)中的连杆![]() 绕点
绕点![]() 逆时针旋转,使
逆时针旋转,使![]() ,如图3,问此时连杆端点
,如图3,问此时连杆端点![]() 离桌面
离桌面![]() 的高度是增加了还是减少?增加或减少了多少?(精确到
的高度是增加了还是减少?增加或减少了多少?(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com