
【题目】已知:如图,∠AGB=∠EHF,∠C=∠D.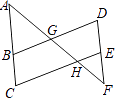
(1)求证:BC∥DE.
(2)求证:∠A=∠F.
【答案】
(1)证明:∵∠AGB=∠EHF=∠AHC,
∴BD∥CE,
∴∠D=∠CEF,
又∵∠C=∠D,
∴∠C=∠CEF,
∴BC∥DE;
(2)证明:∵BC∥DE,
∴∠A=∠F.
【解析】(1)先证明∠AGB=∠EHF=∠AHC,然后依据平行线的判定定理可得到BD∥CE,然后依据平行线的性质可得到∠D=∠CEF,再根据∠C=∠D,得到∠C=∠CEF,最后,再依据平行线的判定定理BC∥DE;
(2)根据两直线平行,内错角相等进行证明即可.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
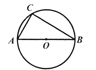
【题目】(10分)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8.
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E.求出由线段ED,BE,![]() 所围成区域的面积.(其中
所围成区域的面积.(其中![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
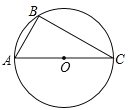
【题目】如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°.
(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求△ABE与△CDE的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,正方形ABCD的对角线AC,BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F. 
(1)求证:OE=OF;
(2)若正方形ABCD的对角线长为4,求两个正方形重叠部分的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成计算:
(1)先化简,再求值:(4ab3﹣8a2b2)÷4ab+(2a+b)(2a﹣b),其中a=2,b=1.
(2)因式分解:3x2﹣6axy+3ay2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N
(1)求证:AE=MN;
(2)若AE=2,∠DAE=30°,求正方形的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com