
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
Θ®1Θ©Βψ![]() ¥”Βψ
¥”Βψ![]() ΩΣ Φ―Ί
ΩΣ Φ―Ί![]() ±Ώœρ
±Ώœρ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·Θ§Βψ
ΒΡΥΌΕ»“ΤΕ·Θ§Βψ![]() ¥”
¥”![]() ΒψΩΣ Φ―Ί
ΒψΩΣ Φ―Ί![]() ±ΏœρΒψ
±ΏœρΒψ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·.»γΙϊΒψ
ΒΡΥΌΕ»“ΤΕ·.»γΙϊΒψ![]() Θ§
Θ§![]() Ζ÷±π¥”
Ζ÷±π¥”![]() Θ§
Θ§![]() Ά§ ±≥ωΖΔΘ§Ψ≠ΙΐΦΗΟκΘ§
Ά§ ±≥ωΖΔΘ§Ψ≠ΙΐΦΗΟκΘ§![]() ΒΡΟφΜΐΒ»”Ύ
ΒΡΟφΜΐΒ»”Ύ![]() ΘΩ
ΘΩ
Θ®2Θ©Βψ![]() ¥”Βψ
¥”Βψ![]() ΩΣ Φ―Ί
ΩΣ Φ―Ί![]() ±ΏœρΒψ
±ΏœρΒψ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·Θ§Βψ
ΒΡΥΌΕ»“ΤΕ·Θ§Βψ![]() ¥”
¥”![]() ΒψΩΣ Φ―Ί
ΒψΩΣ Φ―Ί![]() ±ΏœρΒψ
±ΏœρΒψ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·.»γΙϊΒψ
ΒΡΥΌΕ»“ΤΕ·.»γΙϊΒψ![]() Θ§
Θ§![]() Ζ÷±π¥”
Ζ÷±π¥”![]() Θ§
Θ§![]() Ά§ ±≥ωΖΔΘ§œΏΕΈ
Ά§ ±≥ωΖΔΘ§œΏΕΈ![]() ΡήΖώΫΪ
ΡήΖώΫΪ![]() Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷ΘΩ»τΡήΘ§«σ≥ω‘ΥΕ· ±ΦδΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”….
Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷ΘΩ»τΡήΘ§«σ≥ω‘ΥΕ· ±ΦδΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”….
Θ®3Θ©»τΒψ![]() ―ΊœΏΕΈ
―ΊœΏΕΈ![]() ΖΫœρ¥”
ΖΫœρ¥”![]() Βψ≥ωΖΔ“‘
Βψ≥ωΖΔ“‘![]() ΒΡΥΌΕ»œρΒψ
ΒΡΥΌΕ»œρΒψ![]() “ΤΕ·Θ§Βψ
“ΤΕ·Θ§Βψ![]() ―Ί…δœΏ
―Ί…δœΏ![]() ΖΫœρ¥”
ΖΫœρ¥”![]() Βψ≥ωΖΔ“‘
Βψ≥ωΖΔ“‘![]() ΒΡΥΌΕ»“ΤΕ·Θ§
ΒΡΥΌΕ»“ΤΕ·Θ§![]() Θ§
Θ§![]() Ά§ ±≥ωΖΔΘ§Έ ΦΗΟκΚσΘ§
Ά§ ±≥ωΖΔΘ§Έ ΦΗΟκΚσΘ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() ΘΩ
ΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©2ΟκΜρ4Οκ Θ®2Θ©¥πΑΗΦϊΫβΈω Θ®3Θ©![]() ΟκΜρ5Οκ
ΟκΜρ5Οκ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί÷±Ϋ«»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΚΆ¬Ζ≥Χ=ΥΌΕ»ΓΝ ±ΦδΫχ––«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©…ηΨ≠Ιΐ![]() ΟκΘ§œΏΕΈ
ΟκΘ§œΏΕΈ![]() ΡήΖώΫΪ
ΡήΖώΫΪ![]() Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§ΗυΨίΟφΜΐ÷°ΦδΒΡΒ»ΝΩΙΊœΒΚΆ≈–±π ΫΦ¥Ω…«σΫβΘΜ
Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§ΗυΨίΟφΜΐ÷°ΦδΒΡΒ»ΝΩΙΊœΒΚΆ≈–±π ΫΦ¥Ω…«σΫβΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΘΚΔΌΒ±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ ±ΘΜ
…œ ±ΘΜ
ΔΎΒ±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() ΒΡ―”≥ΛœΏ…œ ±Θ§Ϋχ––Χ÷¬έΦ¥Ω…«σΫβ.
ΒΡ―”≥ΛœΏ…œ ±Θ§Ϋχ––Χ÷¬έΦ¥Ω…«σΫβ.
ΫβΘΚΘ®1Θ©…ηΨ≠Ιΐ![]() ΟκΘ§
ΟκΘ§![]() ΒΡΟφΜΐΒ»”Ύ
ΒΡΟφΜΐΒ»”Ύ![]() Θ§“άΧβ“β”–
Θ§“άΧβ“β”–
![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§![]() Θ§
Θ§
Ψ≠Φλ―ιΘ§![]() Θ§
Θ§![]() ΨυΖϊΚœΧβ“β.
ΨυΖϊΚœΧβ“β.
¥πΘΚΨ≠Ιΐ2ΟκΜρ4ΟκΘ§![]() ΒΡΟφΜΐΒ»”Ύ
ΒΡΟφΜΐΒ»”Ύ![]() .
.
Θ®2Θ©…ηΨ≠Ιΐ![]() ΟκΘ§œΏΕΈ
ΟκΘ§œΏΕΈ![]() ΫΪ
ΫΪ![]() Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§“άΧβ“β”–
Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§“άΧβ“β”–
![]() Θ§
Θ§
Μ·ΦρΩ…ΒΟ![]() .
.
ΓΏ![]() .Γύ¥ΥΖΫ≥ΧΈό Β ΐΗυ.
.Γύ¥ΥΖΫ≥ΧΈό Β ΐΗυ.
ΓύœΏΕΈ![]() ≤ΜΡήΫΪ
≤ΜΡήΫΪ![]() Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷.
Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷.
Θ®3Θ©Β±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ ±Θ§
…œ ±Θ§
…ηΨ≠Ιΐ![]() ΟκΘ§
ΟκΘ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() .
.
“άΧβ“β”–![]() Θ§
Θ§![]()
ΫβΒΟ![]() Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§![]() Θ§
Θ§
Γύ![]() ΘΜ
ΘΜ
Β±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() ΒΡ―”≥ΛœΏ…œ ±Θ§
ΒΡ―”≥ΛœΏ…œ ±Θ§
…ηΨ≠Ιΐ![]() ΟκΘ§
ΟκΘ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() .
.
“άΧβ“β”–![]() Θ§
Θ§![]() Θ§
Θ§
ΫβΒΟ![]() .
.
Ψ≠Φλ―ιΘ§![]() ΖϊΚœΧβ“β.
ΖϊΚœΧβ“β.
Ήέ…œΥυ ωΘ§Ψ≠Ιΐ![]() ΟκΜρ5ΟκΘ§
ΟκΜρ5ΟκΘ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
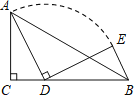
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ADΓΔBE «÷–œΏΘ§ΥϋΟ«œύΫΜ”ΎΒψFΘ§EGΓΈBCΘ§ΫΜAD”ΎΒψGΘ°
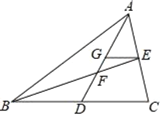
Θ®1Θ©«σ÷ΛΘΚΓςFGEΓΉΓςFDBΘΜ
Θ®2Θ©«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“ΜΗωΙΑ–Έ«≈ΦήΩ…“‘ΫϋΥΤΩ¥Ής «”…Β»―ϋΧί–ΈABD8D1ΚΆΤδ…œΖΫΒΡ≈ΉΈοœΏD1OD8Ήι≥….»τΫ®ΝΔ»γΆΦΥυ ΨΒΡ÷±Ϋ«Ήχ±ξœΒΘ§ΩγΕ»AB=44ΟΉΘ§ΓœA=45ΓψΘ§AC1=4ΟΉΘ§ΒψD2ΒΡΉχ±ξΈΣ(-13Θ§-1.69)Θ§‘ρ«≈ΦήΒΡΙΑΗΏOH=________ΟΉ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
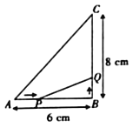
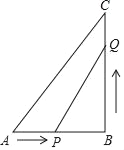
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœB=90ΓψΘ§AB=5cmΘ§BC=7cmΘ°ΒψP¥”ΒψAΩΣ Φ―ΊAB±ΏœρΒψB“‘1cm/sΒΡΥΌΕ»“ΤΕ·Θ§ΒψQ¥”ΒψBΩΣ Φ―ΊBC±ΏœρΒψC“‘2cm/sΒΡΥΌΕ»“ΤΕ·Θ°
Θ®1Θ©»γΙϊPΘ§QΖ÷±π¥”AΘ§BΆ§ ±≥ωΖΔΘ§Ρ«Ο¥ΦΗΟκΚσΘ§ΓςPBQΒΡΟφΜΐΒ»”Ύ6cm2ΘΩ
Θ®2Θ©‘ΎΘ®1Θ©÷–Θ§ΓςPQBΒΡΟφΜΐΡήΖώΒ»”Ύ8cm2ΘΩΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…ΧΒξΙΚΫχ“Μ≈ζΒΞΦέΈΣ16‘ΣΒΡ»’”ΟΤΖ,œζ έ“ΜΕΈ ±ΦδΚσ,ΈΣΝΥΜώ»ΓΗϋΕύάϊ»σ, …ΧΒξΨωΕ®ΧαΗΏœζ έΦέΗώ,Ψ≠ ‘―ιΖΔœ÷,»τΑ¥ΟΩΦΰ20‘ΣΒΡΦέΗώœζ έ ±,ΟΩ‘¬Ρή¬τ360Φΰ; »τΑ¥ΟΩΦΰ25‘ΣΒΡΦέΗώœζ έ ±,ΟΩ‘¬Ρή¬τ210Φΰ.ΦΌΕ®ΟΩ‘¬œζ έΦΰ ΐy(Φΰ) «ΦέΗώx( ‘Σ/Φΰ)ΒΡ“Μ¥ΈΚ· ΐ.
(1) ‘«σy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ Ϋ;
(2)‘Ύ…ΧΤΖ≤ΜΜΐ―Ι,«“≤ΜΩΦ¬«ΤδΥϊ“ρΥΊΒΡΧθΦΰœ¬,Έ œζ έΦέΗώΈΣΕύ…Ό ±,≤≈Ρή ΙΟΩ‘¬ΜώΒΟΉν¥σάϊ»σ?ΟΩ‘¬ΒΡΉν¥σάϊ»σ «Εύ…Ό?(Ήήάϊ»σ=Ήή ’»κ-Ήή≥…±Ψ).
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Ε‘”ΎΒψPΘ®xΘ§yΘ©ΚΆQΘ®xΘ§yΓδΘ©Θ§Ηχ≥ω»γœ¬Ε®“εΘΚ»τyΓδΘΫ![]() Θ§‘ρ≥ΤΒψQΈΣΒψPΒΡΓΑΩ…ΩΊ±δΒψΓ±Θ°«κΈ ΘΚ»τΒψP‘ΎΚ· ΐyΘΫ©¹x2+16Θ®©¹5ΓήxΓήaΘ©ΒΡΆΦœσ…œΘ§ΤδΓΑΩ…ΩΊ±δΒψΓ±QΒΡΉίΉχ±ξyΓδΒΡ»Γ÷ΒΖΕΈß «©¹16ΓήyΓδΓή16Θ§‘ρ Β ΐaΒΡ÷Β «____Θ°
Θ§‘ρ≥ΤΒψQΈΣΒψPΒΡΓΑΩ…ΩΊ±δΒψΓ±Θ°«κΈ ΘΚ»τΒψP‘ΎΚ· ΐyΘΫ©¹x2+16Θ®©¹5ΓήxΓήaΘ©ΒΡΆΦœσ…œΘ§ΤδΓΑΩ…ΩΊ±δΒψΓ±QΒΡΉίΉχ±ξyΓδΒΡ»Γ÷ΒΖΕΈß «©¹16ΓήyΓδΓή16Θ§‘ρ Β ΐaΒΡ÷Β «____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘΚ‘ΎΓ―O÷–Θ§ADΤΫΖ÷‘≤÷ήΫ«ΓœBACΘ§AEΓΆBCΘ§ΓœBACΘΫ60ΓψΘ§ΓœOADΘΫ16ΓψΘ§«σΓœCΒΡΕ» ΐΈΣΘ®ΓΓΓΓΘ©
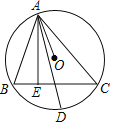
A.50ΓψB.30ΓψC.44ΓψD.45Γψ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ,‘ΎΓςACD÷–,ΓœACDΘΫ90Γψ,ACΘΫb,CDΘΫa,ADΘΫc,ΒψB‘ΎCDΒΡ―”≥ΛœΏ…œ
(1)«σ÷Λ:ΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χ![]() ±Ί”– Β ΐΗυ
±Ί”– Β ΐΗυ
(2)Β±bΘΫ3,CBΘΫ5 ±.ΫΪœΏΕΈAD»ΤΒψDΥ≥ ±’κ–ΐΉΣ90Γψ,ΒΟΒΫœΏΕΈDE,Ν§Ϋ”BE,‘ρΒ±aΒΡ÷ΒΈΣΕύ…Ό ±,œΏΕΈBEΒΡ≥ΛΉνΕΧ,ΉνΕΧ≥ΛΕ» «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΥΒΖ®:ΔΌΈΜΥΤΆΦ–ΈΕΦœύΥΤΘΜΔΎΈΜΥΤΆΦ–ΈΕΦ «ΤΫ“ΤΚσ‘ΌΖ≈¥σ(ΜρΥθ–Γ)ΒΟΒΫΘΜΔέ÷±Ϋ«»ΐΫ«–Έ–±±Ώ…œΒΡ÷–œΏ”κ–±±ΏΒΡ±»ΈΣ1:2ΘΜΔήΝΫΗωœύΥΤΕύ±Ώ–ΈΒΡΟφΜΐ±»ΈΣ4:9Θ§‘ρ÷ή≥ΛΒΡ±»ΈΣ16:81÷–Θ§’ΐ»ΖΒΡ”–( )

A. 1Ηω B. 2Ηω C. 3Ηω D. 4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com