
分析 (1)根据正比例函数的自变量的指数为1且比例系数不为零即可求得m的值,代入求得解析式即可;
(2)将x的值代入求得的解析式即可求得y的值.
解答 解:(1)∵正比例函数y=(2m-1)${x}^{2-{m}^{2}}$中,y随x的增大而减少,
∴$\left\{\begin{array}{l}{2-{m}^{2}=1}\\{2m-1<0}\end{array}\right.$,
解得:m=-1,
∴正比例函数为y=-3x;
(2)当x=$\frac{1}{4}$时,y=-3×$\frac{1}{4}$=-$\frac{3}{4}$.
点评 本题考查了待定系数法求正比例函数的解析式,解题的关键是根据函数的增减性确定反比例函数的系数的符号,难度不大.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
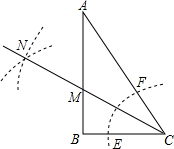 Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
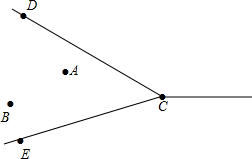 A、B两村坐落在两条相交公路CD、CE内,现计划修建一所小学校,要求学校必须满足下列条件:
A、B两村坐落在两条相交公路CD、CE内,现计划修建一所小学校,要求学校必须满足下列条件:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com