
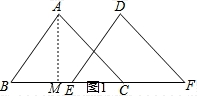
如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a(a<8)个单位到△DEF的位置.
(1)求△ABC的BC边上的高;
(2)连结AE、AD,设AB=5.
①求线段DF的长;
②当△ADE是等腰三角形时,求a的值.
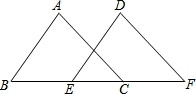
【考点】等腰三角形的判定与性质;勾股定理;平移的性质.
【分析】(1)如图1过点A作AM⊥BC于点M,由三角形的面积公式求得△ABC的BC边上的高是8;
(2)①在Rt△AMB中,由勾股定理求得BM=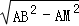 =
=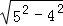 =3,得到CM=BC﹣BM=8﹣3=5,在Rt△AMC中,由勾股定理求得AC=
=3,得到CM=BC﹣BM=8﹣3=5,在Rt△AMC中,由勾股定理求得AC=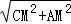 =
=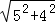 =
=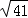 ,得到DF=AC=
,得到DF=AC=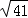 ;②如图2当△ADE是等腰三角形时,分三种情况讨论:当AD=DE时,a=5,当AE=DE时,因为AB=DE,得到AB=AE,BE=2BM=6,求得a=6;当AE=AD时,在Rt△AME中,AM=4,AE=a,ME=a﹣3,由勾股定理得:42+(a﹣3)2=a2,解得:a=
;②如图2当△ADE是等腰三角形时,分三种情况讨论:当AD=DE时,a=5,当AE=DE时,因为AB=DE,得到AB=AE,BE=2BM=6,求得a=6;当AE=AD时,在Rt△AME中,AM=4,AE=a,ME=a﹣3,由勾股定理得:42+(a﹣3)2=a2,解得:a=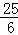 ,
,
【解答】解:(1)如图1过点A作AM⊥BC于点M,
∵△ABC的面积为16,BC=8,
∴ ×8×AM=8,∴AM=4,
×8×AM=8,∴AM=4,
∴△ABC的BC边上的高是8;
(2)①在Rt△AMB中,BM= =
=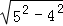 =3,
=3,
∴CM=BC﹣BM=8﹣3=5,
∴在Rt△AMC中,AC=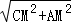 =
=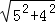 =
=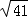 ,
,
∴DF=AC=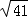 ,
,
②如图2当△ADE是等腰三角形时,有三种情况:
当AD=DE时,a=5,
当AE=DE时,又∵AB=DE,
∴AB=AE,
∴BE=2BM=6,∴a=6;
当AE=AD时,在Rt△AME中,
AM=4,AE=a,ME=a﹣3,
由勾股定理得:42+(a﹣3)2=a2,
解得:a=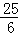 ,
,
综上所述,当△ADE是等腰三角形时,a的值为5或6或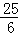 .
.
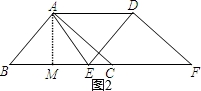
【点评】本题考查了等腰三角形的判定和性质,平移的性质,勾股定理得应用,特别是(2)②要分类讨论否则容易漏解.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,如果全组有x名同学,则根据题意列出的方程是( )
A.x(x+1)=182 B.x(x﹣1)=182 C.x(x+1)=182×2 D.x(x﹣1)=182×2
查看答案和解析>>
科目:初中数学 来源: 题型:
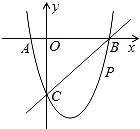
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com