
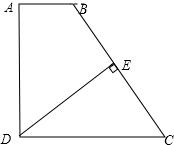
 如图,在直角梯形ABCD中,已知AB∥DC,DE⊥BC,E是BC的中点,探究AB,DC,AD的关系.
如图,在直角梯形ABCD中,已知AB∥DC,DE⊥BC,E是BC的中点,探究AB,DC,AD的关系.  夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
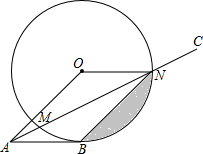 如图,AB切⊙O于点B,AC交⊙O于点M、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm.
如图,AB切⊙O于点B,AC交⊙O于点M、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.
如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| C站 | D站 | 总计 | |
| A乡 | x吨 | 200吨 | |
| B乡 | 300吨 | ||
| 总计 | 240吨 | 260吨 | 500吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
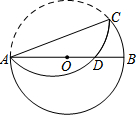 已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.
已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com