
| C站 | D站 | 总计 | |
| A乡 | x吨 | 200吨 | |
| B乡 | 300吨 | ||
| 总计 | 240吨 | 260吨 | 500吨 |
分析 (1)结合已知完善表格,再根据运费=运输单价×数量,得出yA、yB与x的关系式;
(2)令yA=yB,找出二者运费相等的x,以此为界分成三种情况;
(3)由B乡运费最多为4830元,找出x的取值范围,再根据yA+yB的单调性,即可得知当x取什么值时,总运费最低.
解答 解:(1)根据已知补充表格如下:
| C站 | D站 | 总计 | |
| A乡 | x吨 | 200-x吨 | 200吨 |
| B乡 | 240-x吨 | x+60吨 | 300吨 |
| 总计 | 240吨 | 260吨 | 500吨 |
点评 本题考查了一次函数的单调性以及解一元一次不等式,解题的关键是:(1)由运费=运输单价×数量结合表格得出结论;(2)令yA=yB得出x,在分类探讨;(3)由一元一次不等式找出x的取值范围,再根据单调性求最值.本题属于基础题,难度不大,做该类型题目时,要明确条件中的数量关系,找准关系式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
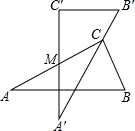 两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.
两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
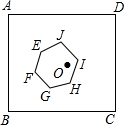 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )| A. | $\frac{\sqrt{2}+1}{2}$ | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{3+2\sqrt{3}}{6}$ | D. | $\frac{3-2\sqrt{3}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com