
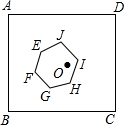
 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )| A. | $\frac{\sqrt{2}+1}{2}$ | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{3+2\sqrt{3}}{6}$ | D. | $\frac{3-2\sqrt{3}}{6}$ |
分析 当正六边形EFGHIJ的边长最大时,要使AE最小,六边形对角线EH与正方形对角线AC重合就可解决问题.
解答 解:如图所示,当EH=AB时,正六边形自由旋转且始终在正方形里,此时正六边形的边长最大,再当EH与正方形对角线AD重合时,AE最小;
∵正方形ABCD的边长为1;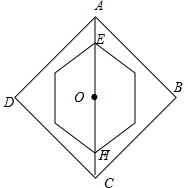
∴AC=$\sqrt{2}$,
∴EH=1,
∴AE=$\frac{\sqrt{2}-1}{2}$,
则AE的最小值为AE=$\frac{\sqrt{2}-1}{2}$.
故选:B.
点评 本题考查了正多边形的性质与运动的轨迹问题,解决本题的关键是首先找到正六边形的边长最大时正六边形在正方形内的位置,再旋转正六边形使得AE最小.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
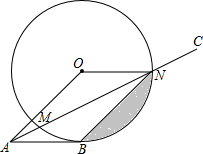 如图,AB切⊙O于点B,AC交⊙O于点M、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm.
如图,AB切⊙O于点B,AC交⊙O于点M、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| C站 | D站 | 总计 | |
| A乡 | x吨 | 200吨 | |
| B乡 | 300吨 | ||
| 总计 | 240吨 | 260吨 | 500吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
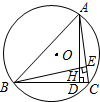 如图,△ABC内接于⊙O,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H.若BC=6,AH=4,则⊙O的半径为$\sqrt{13}$.
如图,△ABC内接于⊙O,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H.若BC=6,AH=4,则⊙O的半径为$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
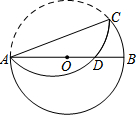 已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.
已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,BF是高,延长CB至点D,使BD=BA,连接AD,过点D作DE⊥AB交AB的延长线于点E,当AF=BE,∠CAD=96°时,∠C=56°.
如图,△ABC中,BF是高,延长CB至点D,使BD=BA,连接AD,过点D作DE⊥AB交AB的延长线于点E,当AF=BE,∠CAD=96°时,∠C=56°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB⊥BD,CD⊥BD.
如图,已知AB⊥BD,CD⊥BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A,作正方形A2B2C2C1,按这样的规律下去,第2012个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A,作正方形A2B2C2C1,按这样的规律下去,第2012个正方形的面积为( )| A. | 5•($\frac{3}{2}$)2010 | B. | 5•($\frac{3}{2}$)4022 | C. | 5•($\frac{9}{4}$)2012 | D. | 5•($\frac{9}{4}$)2010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com