
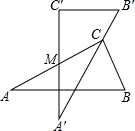
 两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.
两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3. 分析 连接AA′,先由点M是线段AC、线段A′C′的中点可知,AM=MC=A′M=MC′=3,故可得出∠MCA′=∠MA′C=30°,故可得出∠MCB′的度数,根据四边形内角和定理可得出∠C′MC的度数,进而可判断出△AA′M的形状,进而得出结论.
解答 解:连接AA′,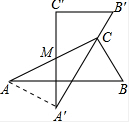
∵点M是线段AC、线段A′C′的中点,AC=6,
∴AM=MC=A′M=MC′=3,
∵∠MA′C=30°,
∴∠MCA′=∠MA′C=30°,
∴∠MCB′=180°-30°=150°,
∴∠C′MC=360°-(∠MCB′+∠B′+∠C′)=180°-(150°+60°+90°)=60°,
∴∠AMA′=∠C′MC=60°,
∴△AA′M是等边三角形,
∴AA′=AM=3,
故答案为:3.
点评 本题考查的是等边三角形的判定与性质,根据题意作出辅助线,构造出等边三角形是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.
如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| C站 | D站 | 总计 | |
| A乡 | x吨 | 200吨 | |
| B乡 | 300吨 | ||
| 总计 | 240吨 | 260吨 | 500吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
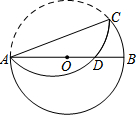 已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.
已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
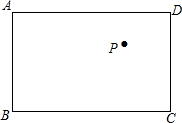 如图,在矩形ABCD中,AB=6,BC=8,P为矩形内一点,PE为点P到直线BC的距离,则PA+PD+PE的最小值为6+4$\sqrt{3}$.
如图,在矩形ABCD中,AB=6,BC=8,P为矩形内一点,PE为点P到直线BC的距离,则PA+PD+PE的最小值为6+4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
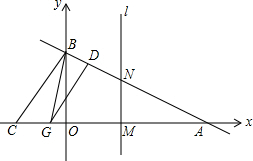 已知:如图,直线y=-$\frac{1}{2}$x+4与x轴交于A点,与y轴交于B点.点C是x轴负半轴上的一点,且满足OC:BC=3:5.
已知:如图,直线y=-$\frac{1}{2}$x+4与x轴交于A点,与y轴交于B点.点C是x轴负半轴上的一点,且满足OC:BC=3:5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com