
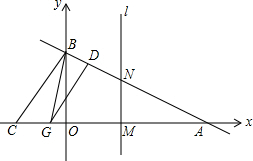
 已知:如图,直线y=-$\frac{1}{2}$x+4与x轴交于A点,与y轴交于B点.点C是x轴负半轴上的一点,且满足OC:BC=3:5.
已知:如图,直线y=-$\frac{1}{2}$x+4与x轴交于A点,与y轴交于B点.点C是x轴负半轴上的一点,且满足OC:BC=3:5.分析 (1)由OC:BC=3:5,设出BC的长度为5a,OC长度为3a,由直线与y轴交点为B,可求出B点坐标,由勾股定理即可求出a的值,从而得出结论;
(2)假设存在,设出P点坐标,由于△ABP是以AB为一条直角边的直角三角形分两种情况,故分两种情况考虑,结合两点间的距离公式及勾股定理即可得出结论;
(3)由相似三角形的性质找出AD的长度,从而得出BD的长度,再结合点到直线的距离与三角形的面积公式即可得出结论.
解答 解:(1)设线段BC的长度为5a,则OC=3a.
令x=0,y=4;
令y=0,-$\frac{1}{2}$x+4=0,解得:x=8.
即点B的坐标为(0,4),点A的坐标为(8,0),
∴OB=4,OA=8.
由勾股定理得:OB=$\sqrt{B{C}^{2}-O{C}^{2}}$=4a=4,
解得:a=1,
故线段BC的长为5.
(2)∵OC=3a=3,
∴点C的坐标为(-3,0),
又∵点C关于原点O对称的点为点M,
∴点M的坐标为(3,0),
∴直线l的解析式为x=3.
假设存在符合条件的点P,设点P坐标为(3,m),
由两点间的距离公式可知:
PA=$\sqrt{(3-8)^{2}+(m-0)^{2}}$,PB=$\sqrt{(3-0)^{2}+(m-4)^{2}}$,AB=$\sqrt{(8-0)^{2}+(0-4)^{2}}$=4$\sqrt{5}$.
以AB为一条直角边的直角三角形分两种情况:
①当∠ABP=90°时,有AB2+PB2=PA2,即8m=80,
解得:m=10,
此时点P坐标为(3,10);
②当∠PAB=90°时,有PA2+AB2=PB2,即-8m=80,
解得:m=-10,
此时点P坐标为(3,-10).
综上可知:在直线l上存在点P,使得△ABP是以AB为一条直角边的直角三角形,点P的坐标为(3,10)或(3,-10).
(3) 直线AB的解析式为y=-$\frac{1}{2}$x+4,即$\frac{1}{2}$x+y-4=0.
直线AB的解析式为y=-$\frac{1}{2}$x+4,即$\frac{1}{2}$x+y-4=0.
点G(t,0)到直线AB的距离h=$\frac{|\frac{1}{2}t-4|}{\sqrt{(\frac{1}{2})^{2}+{1}^{2}}}$=$\frac{2\sqrt{5}}{5}$|$\frac{1}{2}$t-4|,
∵点G在线段AC上,
∴-3≤t≤8,
∴h=$\frac{8\sqrt{5}}{5}$-$\frac{\sqrt{5}}{5}$t.
∵GD∥BC,
∴∠BCA=∠DGA,
又∵∠BAC=∠DAG,
∴△ABC∽△ADG,
∴$\frac{AD}{AB}$=$\frac{AG}{AC}$.
∵点A(8,0),点C(-3,0),点G(t,0),
∴AC=8-(-3)=11,AG=8-t,
又∵AB=4$\sqrt{5}$,
∴AD=$\frac{AG•AB}{AC}$=$\frac{4\sqrt{5}(8-t)}{11}$,
∴BD=AB-AD=$\frac{4\sqrt{5}(3+t)}{11}$.
△BGD的面积为S=$\frac{1}{2}$BD•h=$\frac{1}{2}$×$\frac{4\sqrt{5}(3+t)}{11}$×($\frac{8\sqrt{5}}{5}$-$\frac{\sqrt{5}}{5}$t)=-$\frac{2}{11}$t2+$\frac{10}{11}$t+$\frac{48}{11}$(-3≤t≤8).
点评 本题考查了勾股定理、两点间的距离公式、点到直线的距离、相似三角形的判定及性质和三角形的面积公式,解题的关键:(1)按照比例设出未知数a,结合勾股定理列出关于a的一元一次方程;(2)分哪个角为直角,结合两点间的距离公式和勾股定理得出关于m的一元一次方程;(3)由相似三角形找出BD的长度.本题属于中档题型,(1)难度不大;(2)容易遗漏一种情况造成失分;(3)数据稍显繁琐,需要耐心计算.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
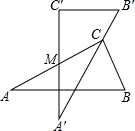 两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.
两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
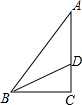 在直角三角形ABC中,BC=6cm,AC=8cm,点D在线段AC上从C向A运动.若设CD=x(m),△ABD的面积为因变量y.
在直角三角形ABC中,BC=6cm,AC=8cm,点D在线段AC上从C向A运动.若设CD=x(m),△ABD的面积为因变量y.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
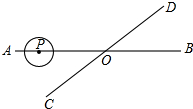 如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的圆P的圆心在直线AB上,且与点O的距离为10cm,如果⊙P以2cm∕s的速度,沿由A向B的方向移动,那么4或6秒钟后⊙P与直线CD相切.
如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的圆P的圆心在直线AB上,且与点O的距离为10cm,如果⊙P以2cm∕s的速度,沿由A向B的方向移动,那么4或6秒钟后⊙P与直线CD相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com