8.阅读下列材料:
北京市统计局发布了2014年人口抽样调查报告,首次增加了环线人口分布数据.调查数据显示,北京市超过一半的常住人口都住在了远离城区的五环以外.事实上,北京市的中心城区人口从上世纪80年代起就持续下降,越来越多的人向郊区迁移.
根据2014年人口抽样调查结果发现,本市三环至六环间,聚集了1226.9万人的常住人口,占全市的57.1%;四环至六环间聚集了941万人的常住人口,占全市的43.8%;五环以外有1098万人的常住人口,占全市的51.1%.
在进行人口分布研究时,北京通常被划分为四个区域,城市功能拓展区包括:朝阳、海淀、丰台、石景山四个区; 城市发展新区包括:通州、顺义、大兴、昌平、房山五个区和亦庄开发区; 首都功能核心区包括:东城区和西城区; 生态涵养发展区包括:门头沟、平谷、怀柔、密云、延庆五个区县.
从常住人口分布上看:城市功能拓展区常住人口最多,占全市总量的49%;城市发展新区常住人口约为684万人;首都功能核心区常住人口约为221万人;生态涵养发展区常住人口约为191万人.
从常住外来人口分布上看:城市功能拓展区常住外来人口最多,约为436万人;城市发展新区常住外来人口约为297万人;首都功能核心区常住外来人口约为54万人;生态涵养发展区常住外来人口约为32万人.
根据以上材料回答下列问题:
(1)估算2014年北京市常住人口约为2149万人.
(2)选择统计表或统计图,将2014年北京市按四个区域的常住人口和常住外来人口分布情况表示出来.
分析 (1)用本市三环至六环间1226.9万人的常住人口除以其占全市的百分比可得;
(2)列表可得.
解答 解:(1)2014年北京市常住人口约为:$\frac{1226.9}{57.1%}$≈2149(万人);
(2)如表所示:
| 城市功能拓展区 | 城市发展新区 | 首都功能核心区 | 生态涵养发展区 |
| 常住人口 | 1053 | 684 | 221 | 191 |
| 常住外来人口 | 436 | 297 | 54 | 32 |
故答案为:(1)2149.
点评 本题主要考查统计图表的选择与制作,根据题意理清其涉及的数量关系是制表的关键.

 阅读快车系列答案
阅读快车系列答案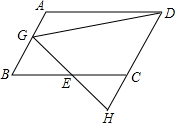 如图,在?ABCD中,E为BC中点,过点E作EG⊥AB于G,连结DG,延长DC,交GE的延长线于点H.已知BC=10,∠GDH=45°,DG=8$\sqrt{2}$.求CD的长.
如图,在?ABCD中,E为BC中点,过点E作EG⊥AB于G,连结DG,延长DC,交GE的延长线于点H.已知BC=10,∠GDH=45°,DG=8$\sqrt{2}$.求CD的长.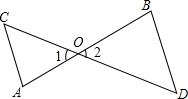 如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.
如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.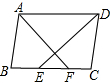 如图,在四边形ABCD中,AB=CD,∠ADC与∠BAD的平分线分别交BC于点E、F,且AF⊥DE,垂足为G
如图,在四边形ABCD中,AB=CD,∠ADC与∠BAD的平分线分别交BC于点E、F,且AF⊥DE,垂足为G