
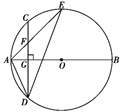
【题目】如图,AB是☉O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=
,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=![]() ;④S△ADF=6
;④S△ADF=6![]() .
.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】分析:①利用垂径定理可知![]() ,可知∠ADF=∠AED,结合公共角可证明△ADF∽△AED;②结合CF=2,且
,可知∠ADF=∠AED,结合公共角可证明△ADF∽△AED;②结合CF=2,且![]() ,可求得DF=6,且CG=DG,可求得FG=2;③在Rt△AGF中可求得AG,在Rt△AGD中可求得tanADG=
,可求得DF=6,且CG=DG,可求得FG=2;③在Rt△AGF中可求得AG,在Rt△AGD中可求得tanADG=![]() ,且∠E=∠ADG,可判断出③;④可先求得S△ADF,再求得△ADF∽△AED的相似比,可求出S△ADE=7
,且∠E=∠ADG,可判断出③;④可先求得S△ADF,再求得△ADF∽△AED的相似比,可求出S△ADE=7![]() .
.
详解:①∵AB为直径,AB⊥CD,
∴![]() ,
,
∴∠ADF=∠AED,且∠FAD=∠DAE,
∴△ADF∽△AED,
∴①正确;
②∵AB为直径,AB⊥CD,
∴CG=DG,
∵![]() ,且CF=2,
,且CF=2,
∴FD=6,
∴CD=8,
∴CG=4,
∴FG=CG-CF=4-2=2,
∴②错误;
③在Rt△AGF中,AF=3,FG=2,
∴AG=![]() ,且DG=4,
,且DG=4,
∴tan∠ADG=![]() ,
,
∵∠E=∠ADG,
∴tan∠E=![]() ,
,
∴③错误;
④在Rt△ADG中,AG=![]() ,DG=4,
,DG=4,
∴AD=![]() ,
,
∴![]() ,
,
∴△ADF∽△AED中的相似比为![]() ,
,
∴![]() ,
,
在△ADF中,DF=6,AG=![]() ,
,
∴S△ADF=![]() DFAG=
DFAG=![]() ×6×
×6×![]() =3
=3![]() ,
,
∴![]() ,
,
∴S△ADE=7![]() ,
,
∴④错误;
∴正确的有①一个.
故选:A.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路:

(1)请你按照他们的解题思路过程完成解答过程;
(2)填空:在△DEF中,DE=15,EF=13,DF=4,则△DEF的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解本校学生喜爱的球类运动,在本校范围内随机调查了部分学生,将收集的 数据绘制成如下两幅不完整的统计图.请你根据图中提供的信息解答下列问题:

(1)本次一共调查了多少名学生?
(2)补全条形统计图,并求出“足球”在扇形统计图中所占圆心角的度数;
(3)若已知该校有 500 名学生,请你根据调查的结果估计爱好“足球”和“排球”的学生共有多 少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解全国中学生最喜爱哪位歌手,适合全面调查.
B.甲乙两种麦种,连续3年的平均亩产量相同,它们的方差为:S甲2=5,S乙2=0.5,则甲麦种产量比较稳.
C.某次朗读比赛中预设半数晋级,某同学想知道自己是否晋级,除知道自己的成绩外,还需要知道平均成绩.
D.一组数据:3,2,5,5,4,6的众数是5.
查看答案和解析>>
科目:初中数学 来源: 题型:
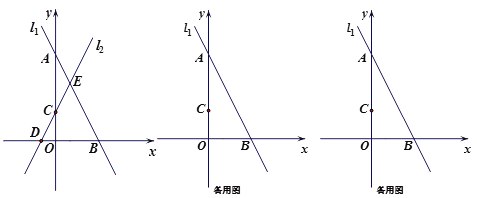
【题目】在平面直角坐标系中,直线l1:![]() 与坐标轴交于A,B两点,直线l2:
与坐标轴交于A,B两点,直线l2:![]() (
(![]() ≠0)与坐标轴交于点C,D.
≠0)与坐标轴交于点C,D.
(1)求点A,B的坐标;
(2)如图,当![]() =2时,直线l1,l2与相交于点E,求两条直线与
=2时,直线l1,l2与相交于点E,求两条直线与![]() 轴围成的△BDE的面积;
轴围成的△BDE的面积;
(3)若直线l1,l2与![]() 轴不能围成三角形,点P(a,b)在直线l2:
轴不能围成三角形,点P(a,b)在直线l2:![]() (k≠0)上,且点P在第一象限.
(k≠0)上,且点P在第一象限.
①求![]() 的值;
的值;
②若![]() ,,求
,,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与![]() 轴相交于点C(0,6),与直线OA相交于点A且点A纵坐标为2,动点P沿路线O
轴相交于点C(0,6),与直线OA相交于点A且点A纵坐标为2,动点P沿路线O![]() A
A![]() C运动.
C运动.
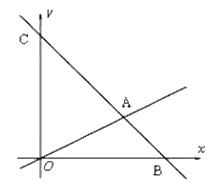
(1)求直线BC的解析式.
(2)求![]() 的面积.
的面积.
(3)当![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 时,求出这时点P的坐标.
时,求出这时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com