
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
【答案】(1)![]()
(2)﹣1<x<0或x>1。
(3)首先求出OA的长度,结合题意CB∥OA且CB=![]() ,判断出四边形OABC是平行四边形,再证明OA=OC。
,判断出四边形OABC是平行四边形,再证明OA=OC。
【解析】
(1)设反比例函数的解析式为![]() (k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式。
(k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式。
(2)直接由图象得出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)首先求出OA的长度,结合题意CB∥OA且CB=![]() ,判断出四边形OABC是平行四边形,再证明OA=OC
,判断出四边形OABC是平行四边形,再证明OA=OC
解:(1)设反比例函数的解析式为![]() (k>0)
(k>0)
∵A(m,﹣2)在y=2x上,∴﹣2=2m,∴解得m=﹣1。∴A(﹣1,﹣2)。
又∵点A在![]() 上,∴
上,∴![]() ,解得k=2。,
,解得k=2。,
∴反比例函数的解析式为![]() 。
。
(2)观察图象可知正比例函数值大于反比例函数值时自变量x的取值范围为﹣1<x<0或x>1。
(3)四边形OABC是菱形。证明如下:
∵A(﹣1,﹣2),∴![]() 。
。
由题意知:CB∥OA且CB=![]() ,∴CB=OA。
,∴CB=OA。
∴四边形OABC是平行四边形。
∵C(2,n)在![]() 上,∴
上,∴![]() 。∴C(2,1)。
。∴C(2,1)。
∴![]() 。∴OC=OA。
。∴OC=OA。
∴平行四边形OABC是菱形。


科目:初中数学 来源: 题型:
【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 ![]() ,导致了第一次数学危机,
,导致了第一次数学危机, ![]() 是无理数的证明如下: 假设
是无理数的证明如下: 假设 ![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成 ![]() (p与q是互质的两个正整数).于是(
(p与q是互质的两个正整数).于是( ![]() )2=(
)2=( ![]() )2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“
)2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“ ![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以, ![]() 是无理数.
是无理数.
这种证明“ ![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法
B.反证法
C.举反例法
D.数学归纳法
查看答案和解析>>
科目:初中数学 来源: 题型:
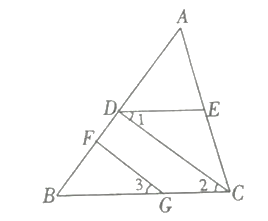
【题目】(1)如图,设![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() ;
;
(2)若把(1)的题设中的“![]() ”与结论中的“
”与结论中的“![]() ”对调后,命题还成立吗?说明理由;
”对调后,命题还成立吗?说明理由;
(3)若把(1)的题设中的“![]() ”与结论中的“
”与结论中的“![]() ”对调后,命题还成立吗?说明理由.
”对调后,命题还成立吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )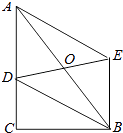
A.4
B.2 ![]()
C.2
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m。设AD的长为xm,DC的长为ym。
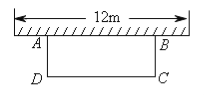
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
销售价格x | 20 | 25 | 30 | 50 |
销售量y | 15 | 12 | 10 | 6 |
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式;
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.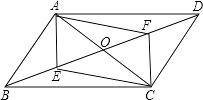
(1)求证:四边形AECF是平行四边形;
(2)如果E,F点分别在DB和BD的延长线上时,且满足BE=DF,上述结论仍然成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com