
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )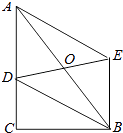
A.4
B.2 ![]()
C.2
D.6
【答案】A
【解析】解:∵在Rt△ABC中,∠B=90°,
∴BC⊥AC.
∵四边形ADBE是平行四边形,
∴OD=OE,OA=OB.
∴当OD取最小值时,DE线段最短,此时OD⊥BC.
∴OD∥CB.
又点O是AB的中点,
∴OD是△ABC的中位线,
∴OD= ![]() CB=2,
CB=2,
∴ED=2OD=4.
所以答案是:A.
【考点精析】本题主要考查了垂线段最短和三角形中位线定理的相关知识点,需要掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】我市某重点中学校团委、学生会发出倡议,在初中各年级捐款购买书籍送给我市贫困地区的学校.初一年级利用捐款买甲、乙两种自然科学书籍若干本,用去5324元;初二年级买了A、B两种文学书籍若干本,用去4840元,其中A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同.若甲、乙两种书的单价之和为121元,则初一和初二两个年级共向贫困地区的学校捐献了________本书.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图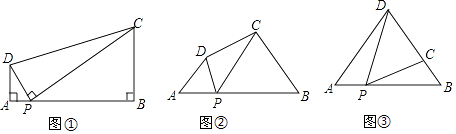
(1)问题:如图①,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:ADBC=APBP.
(2)探究:如图②,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图③,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A,设点P的运动时间为t秒,当以D为圆心,以DC为半径的圆与AB相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D落在点H的位置上,点C恰好落在边AD上的点G处,连接EG.
(1)△GEF是等腰三角形吗?请说明理由;
(2)若CD=4,GD=8,求HF的长度.
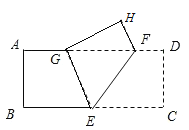
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D
(1)如图1,求证:BD=ED; 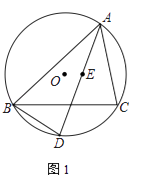
(2)如图2,AD为⊙O的直径.若BC=6,sin∠BAC= ![]() ,求OE的长.
,求OE的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为6,BC=4,AB=12.
(1)求点A、B对应的数;
(2)动点P、Q分别同时从A、C出发,分别以每秒6个单位和3个单位的速度沿数轴正方向运动.M为AP的中点,N在CQ上,且CN=![]() CQ,设运动时间为t(t>0).
CQ,设运动时间为t(t>0).
①求点M、N对应的数(用含t的式子表示); ②t为何值时,OM=2BN.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,∠ABC=90,AE∥CD交BC于E,O是AC的中点,AB=![]() ,AD=2,BC=3,下列结论:
,AD=2,BC=3,下列结论:
①∠CAE=30;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是()

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD.

(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com