
【题目】如图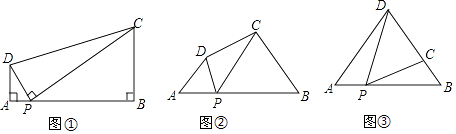
(1)问题:如图①,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:ADBC=APBP.
(2)探究:如图②,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图③,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A,设点P的运动时间为t秒,当以D为圆心,以DC为半径的圆与AB相切时,求t的值.
【答案】
(1)证明:∵∠DPA+∠CPB=90°,∠DPA+∠ADP=90°,
∴∠PDA=∠CPB,
又∵∠A=∠B=90°,
∴△ADP∽△BPC,
∴ ![]() =
=![]() ,
,
∴AD·BC=AP·BP.
(2)解:结论:ADBC=APBP仍然成立,
理由:∵∠ADP+∠APD=180°﹣θ,∠DPA+∠CPB=180°﹣θ,
∴∠ADP=∠CPB,
又∵∠A=∠B=θ,
∴△ADP∽△BPC,
∴ ![]() =
=![]() ,
,
∴AD·BC=AP·BP.
(3)解:作DE⊥AB,当⊙D与AB相切时,半径r=DE=DC,
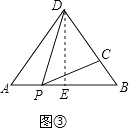
∴DE=![]() =4,
=4,
∴DC=4,
∴BC=1,
依据(1)(2)的结论AD·BC=AP·BP,
∴5×1=t(6﹣t),
∴t2﹣6t+5=0,
解得:t1=1,t2=5,
∴点P运动时间为1s或5s.
【解析】(1)由同角的余角相等得∠PDA=∠CPB,根据相似三角形的判定得△ADP∽△BPC,再由相似三角形的性质得出![]()
![]()
![]() =
=![]() ,即AD·BC=AP·BP.
,即AD·BC=AP·BP.
(2)结论:AD·BC=AP·BP仍然成立;理由:由等量代换得∠ADP=∠CPB,根据相似三角形的判定得△ADP∽△BPC,再由相似三角形的性质得出![]() =
=![]() ,即AD·BC=AP·BP.
,即AD·BC=AP·BP.
(3)作DE⊥AB,当⊙D与AB相切时,半径r=DE=DC,由勾股定理得DE=DC=4,依据(1)(2)的结论AD·BC=AP·BP,即t2﹣6t+5=0,解之即可得出答案.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 ![]() ,导致了第一次数学危机,
,导致了第一次数学危机, ![]() 是无理数的证明如下: 假设
是无理数的证明如下: 假设 ![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成 ![]() (p与q是互质的两个正整数).于是(
(p与q是互质的两个正整数).于是( ![]() )2=(
)2=( ![]() )2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“
)2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“ ![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以, ![]() 是无理数.
是无理数.
这种证明“ ![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法
B.反证法
C.举反例法
D.数学归纳法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
造成医患关系紧张的原因(单选) |
根据调查结果绘制出了如下两幅尚不完整的统计图.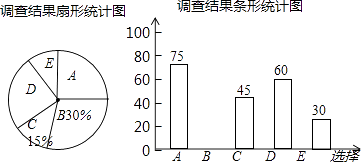
根据以上信息解答下列问题:
(1)这次接受调查的总人数为人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,设![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() ;
;
(2)若把(1)的题设中的“![]() ”与结论中的“
”与结论中的“![]() ”对调后,命题还成立吗?说明理由;
”对调后,命题还成立吗?说明理由;
(3)若把(1)的题设中的“![]() ”与结论中的“
”与结论中的“![]() ”对调后,命题还成立吗?说明理由.
”对调后,命题还成立吗?说明理由.
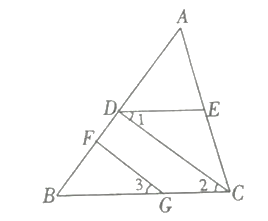
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )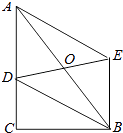
A.4
B.2 ![]()
C.2
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com