
【题目】已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D
(1)如图1,求证:BD=ED; 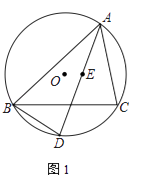
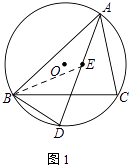
(2)如图2,AD为⊙O的直径.若BC=6,sin∠BAC= ![]() ,求OE的长.
,求OE的长. 
【答案】
(1)证明:连接BE.
∵是△ABC的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
∵∠DBC=∠CAD.
∴∠DBC=∠BAD.
∵∠BED=∠BAD+∠ABE,
∴∠DBE=∠DEB.
∴BD=ED.
(2)解:如图2所示;连接OB.

∵AD是直径,A平分∠BAC,
∴AD⊥BC,且BD=FC=3.
∵∠BAC=∠BOD,sin∠BAC= ![]() ,BF=3,
,BF=3,
∴OB=5.
∵在Rt△BOF中,BF=3,OB=5,
∴OF= ![]() =4.
=4.
∴DF=1.
在Rt△BDF中,BF2+DF2=BD2.
∴BD= ![]() .
.
∴DE= ![]() .
.
使用OE=5﹣ ![]() .
.
【解析】(1)连接BE.依据三角形的内心的性质以及圆周角定理证明∠DBE=∠DEB即可;(2)连接OB.先证明圆周角定理和三角形的内心的性质可知∠BAC=∠BOF,依据锐角三角函数的定义可求得OB的长,然后依据勾股定理可求得OF的长于是得到DF的长,接下来,在△BDF中,由勾股定理可求得BD的长,依据问题(1)的结论可得到DE的长,从而求得OE的长.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,A、B两地相距200km,一列火车从B地出发沿BC方向以![]() 的速度行驶,在行驶过程中,这列火车离A地的路程
的速度行驶,在行驶过程中,这列火车离A地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数关系式是______.
之间的函数关系式是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
造成医患关系紧张的原因(单选) |
根据调查结果绘制出了如下两幅尚不完整的统计图.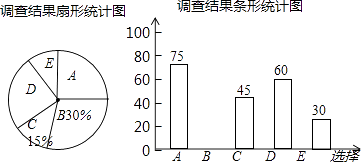
根据以上信息解答下列问题:
(1)这次接受调查的总人数为人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
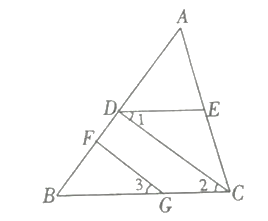
【题目】(1)如图,设![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() ;
;
(2)若把(1)的题设中的“![]() ”与结论中的“
”与结论中的“![]() ”对调后,命题还成立吗?说明理由;
”对调后,命题还成立吗?说明理由;
(3)若把(1)的题设中的“![]() ”与结论中的“
”与结论中的“![]() ”对调后,命题还成立吗?说明理由.
”对调后,命题还成立吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E. 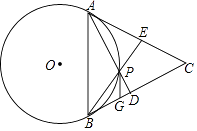
(1)求证:CA,CB是⊙O的切线;
(2)已知AB=6,G在BC上,BG=2,当PG取得最小值时,求PG的长及∠BGP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )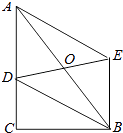
A.4
B.2 ![]()
C.2
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m。设AD的长为xm,DC的长为ym。
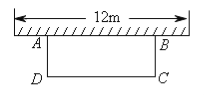
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.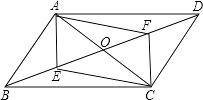
(1)求证:四边形AECF是平行四边形;
(2)如果E,F点分别在DB和BD的延长线上时,且满足BE=DF,上述结论仍然成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
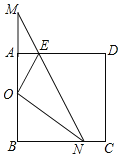
【题目】如图,已知Rt△MBN的两条直角边与正方形ABCD的两邻边重合,∠M=30°,O为AB中点,NO平分∠BNM,EO平分∠AEN.
(1)求证:△MON为等腰三角形;
(2)求证:EN=AE+BN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com