
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m。设AD的长为xm,DC的长为ym。
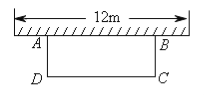
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 都是边长为1的等边三角形.
都是边长为1的等边三角形.
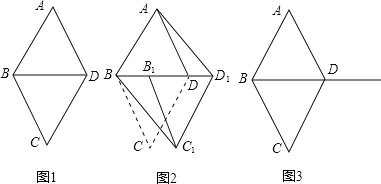
![]() 四边形ABCD是菱形吗?为什么?
四边形ABCD是菱形吗?为什么?
![]() 如图2,将
如图2,将![]() 沿射线BD方向平移到
沿射线BD方向平移到![]() 的位置,则四边形
的位置,则四边形![]() 是平行四边形吗?为什么?
是平行四边形吗?为什么?
![]() 在
在![]() 移动过程中,四边形
移动过程中,四边形![]() 有可能是矩形吗?如果是,请求出点B移动的距离
有可能是矩形吗?如果是,请求出点B移动的距离![]() 写出过程
写出过程![]() ;如果不是,请说明理由
;如果不是,请说明理由![]() 图3供操作时使用
图3供操作时使用![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,点A、B在x轴上,AB⊥BC,AO=OB=2,BC=3
(1)写出点A、B、C的坐标.
(2)如图②,过点B作BD∥AC交y轴于点D,求∠CAB+∠BDO的大小.
(3)如图③,在图②中,作AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D
(1)如图1,求证:BD=ED; 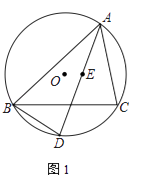
(2)如图2,AD为⊙O的直径.若BC=6,sin∠BAC= ![]() ,求OE的长.
,求OE的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
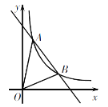
【题目】如图,在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象交于A(1,4),B(3,m)两点.
的图象交于A(1,4),B(3,m)两点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠BOC、∠BOF的度数.
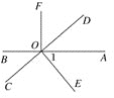
解:∵OE⊥CD( ),
∴∠DOE=_____°( ),
∵∠1=50°( ),
∴∠AOD=∠________-∠________=________°,
∵∠BOC与∠AOD为_______角(____________),
∴∠BOC=∠________=∠_________°(_____________),
∵OD平分∠AOF(______________),
且∠AOD=____________°(______________),
∴∠AOF=2∠__________=________°( ),
∵∠BOF+∠AOF=______°( ),
∴∠BOF=______°-∠AOF=_________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( ) 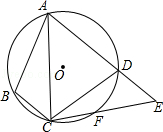
A.60°
B.55°
C.50°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心![]() 出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段
出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段![]() 、(2)半圆弧
、(2)半圆弧![]() 、(3)线段
、(3)线段![]() 后,回到出发点.蚂蚁离出发点的距离
后,回到出发点.蚂蚁离出发点的距离![]() (蚂蚁所在位置与
(蚂蚁所在位置与![]() 点之间线段的长度)与时间
点之间线段的长度)与时间![]() 之间的图象如图2所示,问:(注:圆周率
之间的图象如图2所示,问:(注:圆周率![]() 的值取3)
的值取3)
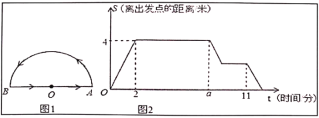
(1)请直接写出:花坛的半径是 米,![]() .
.
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回![]() 所用时间.
所用时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com