
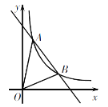
【题目】如图,在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象交于A(1,4),B(3,m)两点.
的图象交于A(1,4),B(3,m)两点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
【答案】(1)y=﹣![]() x+
x+![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)把A代入反比例函数解析式即可求得反比例函数解析式,把点B代入反比例函数解析式就能求得完整的点B的坐标,把A,B坐标代入一次函数即可求得解析式;
(2)把三角形整理为矩形减去若干直角三角形的面积的形式,比较简便.
试题解析:(1)点A(1,4)在反比例函数y=![]() 的图象上,所以k2=xy=1×4=4,故有y=
的图象上,所以k2=xy=1×4=4,故有y=![]() 因为B(3,m)也在y=
因为B(3,m)也在y=![]() 的图象上,
的图象上,
所以m=![]() ,即点B的坐标为B(3,
,即点B的坐标为B(3,![]() ),
),
一次函数y=k1x+b过A(1,4)、B(3,![]() )两点,所以
)两点,所以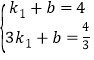
解得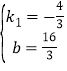 所以所求一次函数的解析式为y=﹣
所以所求一次函数的解析式为y=﹣![]() x+
x+![]()
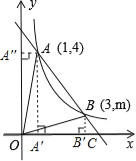
(2)过点A分别作x轴、y轴的垂线,垂足分别为A′、A〞,过点B作x轴的
垂线,垂足为B′,
则S△AOB=S矩形OA′AA″+S梯形A′ABB′﹣S△OAA″﹣S△OBB′
=1×4+![]() ×(4+
×(4+![]() )×(3﹣1)﹣
)×(3﹣1)﹣![]() ×1×4﹣
×1×4﹣![]() ×3×
×3×![]()
=![]() ,
,
∴△AOB的面积为![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧 ![]() 于点P,Q,且点P,Q在AB异侧,连接OP.
于点P,Q,且点P,Q在AB异侧,连接OP. 
(1)求证:AP=BQ;
(2)当BQ=4 ![]() 时,求
时,求 ![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,求OC的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(3,1),B(8,5),若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,请用上述表示法写出另两种走法,并判断这几种走法的路程是否相等。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E. 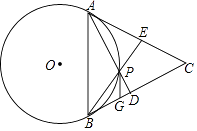
(1)求证:CA,CB是⊙O的切线;
(2)已知AB=6,G在BC上,BG=2,当PG取得最小值时,求PG的长及∠BGP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个10×10的正方形图案,则其中完整的圆共有( )个.
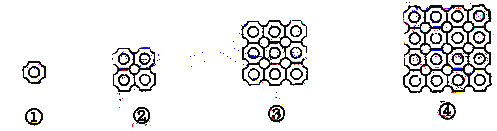
A.145 B.146 C.180 D.181
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m。设AD的长为xm,DC的长为ym。
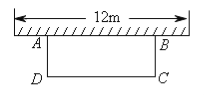
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
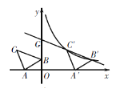
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(d,2).
(1)求d的值;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图象上. 请求出这个反比例函数和此时的直线B′C′的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( ) 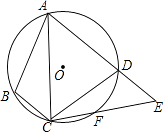
A.45°
B.50°
C.55°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在⊙O中, ![]() =
= ![]() ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC. 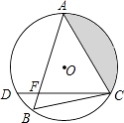
(1)求证:AC2=ABAF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com