
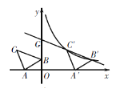
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(d,2).
(1)求d的值;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图象上. 请求出这个反比例函数和此时的直线B′C′的解析式.
【答案】(1)d=-3.(2)y=-![]() x+3.
x+3.
【解析】
(1)过C作CN垂直于x轴,交x轴于点N,由A、B及C的坐标得出OA,OB,CN的长,再证明Rt△CNA≌Rt△AOB,由∠CAB=90°,根据全等三角形的对应边相等可得出CN=0A,AN=0B,由AN+OA求出ON的长,再由C在第二象限,可得出d的值;
(2)由第一问求出的C与B的横坐标之差为3,根据平移的性质得到纵坐标不变,故设出C′(m,2),则B′(m+3,1),再设出反比例函数解析式,将C′与B′的坐标代入得到关于k与m的两方程,消去k得到关于m的方程,求出方程的解得到m的值,即可确定出k的值,得到反比例函数解析式,设直线B′C′的解析式为y=ax+b,将C′与B′的坐标代入,得到关于a与b的二元一次方程组,求出方程组的解得到a与b的值,即可确定出直线B′C′的解析式;
(1)如图,作CN⊥x轴于点N,
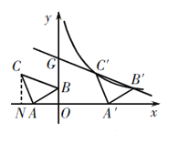
在Rt△CNA和Rt△AOB中,
CN=AO=2,AC=AB,
∴Rt△CNA≌Rt△AOB(HL),
则AN=BO=1,
∴NO=AN+AO=3,且点C在第二象限,
∴d=-3.
(2)设反比例函数为y=![]() ,点C′和B′在该反比例函数图象上,
,点C′和B′在该反比例函数图象上,
设C′(m-3,2),则B′(m,1),
把点C′和B′的坐标分别代入y=![]() ,
,
得k=2m-6,k=m,
∴m=2m-6,
则k=6,m=6,
反比例函数解析式为y=![]() .
.
得点C′(3,2),B′(6,1).
设直线C′B′的解析式为y=ax+b,
把C′、B′两点坐标代入得3a+b=2,6a+b=1,
∴解得a=-![]() ,b=3,
,b=3,
∴直线C′B′的解析式为y=-![]() x+3.
x+3.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:初中数学 来源: 题型:
【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1 , y2 , y3的大小关系为( )
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
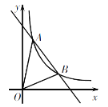
【题目】如图,在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象交于A(1,4),B(3,m)两点.
的图象交于A(1,4),B(3,m)两点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y= ![]() (x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:
(x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:
①逐渐变小;
②由大变小再由小变大;
③由小变大再由大变小;
④不变.
你认为正确的是 . (填序号)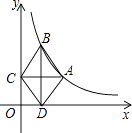
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠BOC、∠BOF的度数.
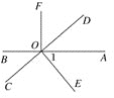
解:∵OE⊥CD( ),
∴∠DOE=_____°( ),
∵∠1=50°( ),
∴∠AOD=∠________-∠________=________°,
∵∠BOC与∠AOD为_______角(____________),
∴∠BOC=∠________=∠_________°(_____________),
∵OD平分∠AOF(______________),
且∠AOD=____________°(______________),
∴∠AOF=2∠__________=________°( ),
∵∠BOF+∠AOF=______°( ),
∴∠BOF=______°-∠AOF=_________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图,EF//AD, ![]() =
=![]() .求证:∠DGA+∠BAC=180°.请将说明过程填写完成.
.求证:∠DGA+∠BAC=180°.请将说明过程填写完成.
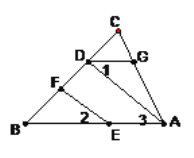
证明:∵EF//AD,(已知)
∴![]() =_____(_____________________________).
=_____(_____________________________).
又∵![]() =
=![]() (______)
(______)
∴![]() =
=![]() (________________________).
(________________________).
∴AB//______(____________________________)
∴∠DGA+∠BAC=180°(_____________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
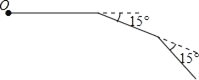
【题目】如图,小明从点O出发,前进5m后向右转15°,再前进5m后又向右转15°,…这样一直下去,直到他第一次回到出发点O为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com