
【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( ) 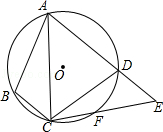
A.60°
B.55°
C.50°
D.45°
【答案】C
【解析】解:∵四边形ABCD内接于⊙O,∠ABC=105°, ∴∠ADC=180°﹣∠ABC=180°﹣110°=70°.
∵且 ![]() =
= ![]() ,∠BAC=20°,
,∠BAC=20°,
∴∠DCE=∠BAC=20°,
∴∠E=∠ADC﹣∠DCE=70°﹣20°=50°.
故选C.
【考点精析】利用圆心角、弧、弦的关系和圆内接四边形的性质对题目进行判断即可得到答案,需要熟知在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
造成医患关系紧张的原因(单选) |
根据调查结果绘制出了如下两幅尚不完整的统计图.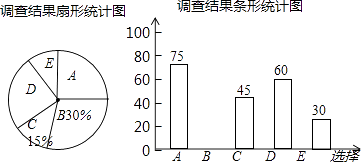
根据以上信息解答下列问题:
(1)这次接受调查的总人数为人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m。设AD的长为xm,DC的长为ym。
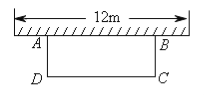
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.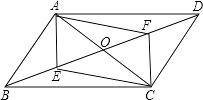
(1)求证:四边形AECF是平行四边形;
(2)如果E,F点分别在DB和BD的延长线上时,且满足BE=DF,上述结论仍然成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( ) 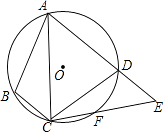
A.45°
B.50°
C.55°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=2![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
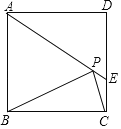
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△MBN的两条直角边与正方形ABCD的两邻边重合,∠M=30°,O为AB中点,NO平分∠BNM,EO平分∠AEN.
(1)求证:△MON为等腰三角形;
(2)求证:EN=AE+BN.
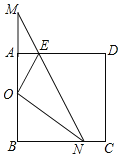
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com