
【题目】如图,已知Rt△MBN的两条直角边与正方形ABCD的两邻边重合,∠M=30°,O为AB中点,NO平分∠BNM,EO平分∠AEN.
(1)求证:△MON为等腰三角形;
(2)求证:EN=AE+BN.
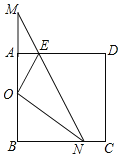
【答案】(1)见解析;(2)见解析.
【解析】
(1) 根据三角形内角和定理、角平分线的性质和等角对等边证得站论.
(2)延长EO交CB的延长线于点P,构造全等三角形; △AOE≌△BOP,结合全等三角形的判定与性质进行解答.
(1)证明:∵∠B=90°,∠M=30°,
∴∠BNM=60°,
∵NO平分∠BNM,
∴∠ONM=![]() ∠BNM=30°,
∠BNM=30°,
∴∠ONM=∠M,
∴OM=ON,
∴MON为等腰三角形;
(2)证明:如图,延长EO交CB延长线于点P.
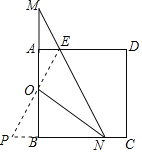
依题意得:∠BAE=∠ABP=90°.
∵O为AB中点,
∴OA=OB,
在△AOE和△BOP中,
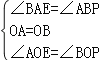 ,
,
∴△AOE≌△BOP(ASA),
∴AE=BP,OE=OP.
又NO平分∠BNM,
∴ON⊥EP,
∴EN=PN,
∴EN=PN=BP+BN=AE+BN,
∴EN=AE+BN.


科目:初中数学 来源: 题型:
【题目】已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D
(1)如图1,求证:BD=ED; 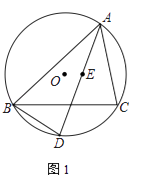
(2)如图2,AD为⊙O的直径.若BC=6,sin∠BAC= ![]() ,求OE的长.
,求OE的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( ) 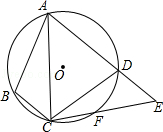
A.60°
B.55°
C.50°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空,并在括号内注明说理依据.
如图,已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 平行吗?
平行吗?![]() 与
与![]() 平行吗?
平行吗?
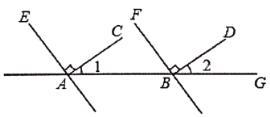
解:因为![]() ,
,![]() (已知),
(已知),
所以![]() .
.
所以 ![]() ( ).
( ).
又因为![]() (已知),
(已知),
所以![]() .( )
.( )
所以![]() .
.
同理可得,![]()
![]() .
.
所以![]() ( ).
( ).
所以 ![]() (同位角相等,两直线平行).
(同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD.

(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心![]() 出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段
出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段![]() 、(2)半圆弧
、(2)半圆弧![]() 、(3)线段
、(3)线段![]() 后,回到出发点.蚂蚁离出发点的距离
后,回到出发点.蚂蚁离出发点的距离![]() (蚂蚁所在位置与
(蚂蚁所在位置与![]() 点之间线段的长度)与时间
点之间线段的长度)与时间![]() 之间的图象如图2所示,问:(注:圆周率
之间的图象如图2所示,问:(注:圆周率![]() 的值取3)
的值取3)
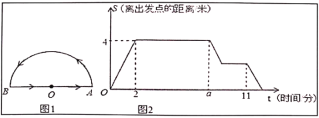
(1)请直接写出:花坛的半径是 米,![]() .
.
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回![]() 所用时间.
所用时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系.

(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系;
(2)将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度a,得到如图2、如图3情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图2证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC. (Ⅰ)求证:直线DM是⊙O的切线;
(Ⅱ)求证:DE2=DFDA.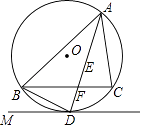
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com