
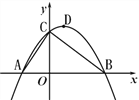
����Ŀ����ͼ,��֪��A������Ϊ��-2��0����ֱ��![]() ��x�ᡢy��ֱ��ڵ�B�͵�C������AC������ΪD��������
��x�ᡢy��ֱ��ڵ�B�͵�C������AC������ΪD��������![]() ��A��B��C����.
��A��B��C����.
��1���������ߵĽ���ʽ������D�����ꣻ
��2���������ߵĶԳ���DE���߶�BC�ڵ�E��P�ǵ�һ��������������һ�㣬����P��x��Ĵ��ߣ����߶�BC�ڵ�F�����ı���DEFPΪƽ���ı��Σ����P������.
��3�����M���߶�BC�ϵ�һ���㣬����M��MN��AB����AC�ڵ�N����Q�ӵ�B��������ÿ��1����λ���ȵ��ٶ����߶�BA���A�˶����˶�ʱ��Ϊt���룩����t���룩Ϊ��ֵʱ�����ڡ�QMNΪ����ֱ�������Σ�
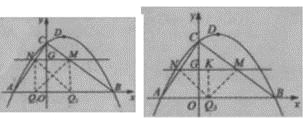
���𰸡���1����1��B��4��O����C��0��3���������ߵĽ���ʽΪ![]() ����D������Ϊ
����D������Ϊ![]() ����2������P����Ϊ��3��
����2������P����Ϊ��3��![]() ��ʱ���ı���DEFPΪƽ���ı��Σ���3����tΪ
��ʱ���ı���DEFPΪƽ���ı��Σ���3����tΪ![]() ��
��![]() ��
��![]() ʱ��������QMNΪ����ֱ�������Σ�
ʱ��������QMNΪ����ֱ�������Σ�
�������������������1����ֱ��y=-![]() +3�Ľ���ʽ���ɵ�B��C��������꣬���ô���ϵ����������������ߵĽ���ʽ�����������ߵĽ���ʽ���ɵ������ߵĽ���ʽ����2�����P����Ϊ
+3�Ľ���ʽ���ɵ�B��C��������꣬���ô���ϵ����������������ߵĽ���ʽ�����������ߵĽ���ʽ���ɵ������ߵĽ���ʽ����2�����P����Ϊ![]() ���F������Ϊ��m��-
���F������Ϊ��m��-![]() m+3���������ı���DEFPΪƽ���ı��Σ���PF=DE���ɴ��з������m��ֵ�����ɵõ�P�����ꣻ��3���ֱ��Ե�M��N��QΪֱ�Ƕ������۽������.
m+3���������ı���DEFPΪƽ���ı��Σ���PF=DE���ɴ��з������m��ֵ�����ɵõ�P�����ꣻ��3���ֱ��Ե�M��N��QΪֱ�Ƕ������۽������.
�����������1��B��4��O����C��0��3����
�����ߵĽ���ʽΪ![]()
����D������Ϊ![]()
��2����x=1����![]()
���PΪ��һ��������������һ�㣬���Կ����P����Ϊ![]()
��F������Ϊ��m��-![]() m+3�������ı���DEFPΪƽ���ı��Σ���PF=DE
m+3�������ı���DEFPΪƽ���ı��Σ���PF=DE
��-![]() m2+
m2+![]() m+3-��-
m+3-��-![]() m+3��=
m+3��=![]()
��֮����m1=3,m2=1���������⣬��ȥ����
������P����Ϊ��3��![]() ��ʱ���ı���DEFPΪƽ���ı��Σ�
��ʱ���ı���DEFPΪƽ���ı��Σ�
��3�����M������Ϊ��n��-![]() ����MN��y���ڵ�G��
����MN��y���ڵ�G��
![]()
![]() ��BAC
��BAC![]()
������Q1MN=90����MN=MQ2=OGʱ��![]() ��֮��MN=2��
��֮��MN=2��
![]() ��֮��
��֮��![]()
����![]() ʱ���������
ʱ���������![]()
![]()
������MQ3N=90����Q3M=Q3Nʱ��![]() NM=Q3K=OG
NM=Q3K=OG
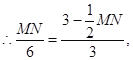 ��֮����MN=3��
��֮����MN=3��
![]()
![]() ��֮����n=2����
��֮����n=2����![]()
MN���е�K������Ϊ![]()
![]() ��
��![]()
����tΪ![]() ��
��![]() ��
��![]() ʱ��������QMNΪ����ֱ�������Σ�
ʱ��������QMNΪ����ֱ�������Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
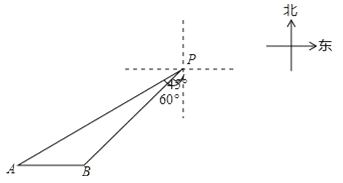
����Ŀ��һ���ִ�λ�ڵ���P��ƫ��60�㷽�������20�����A���������ж��ٺ��ﵽ�����P��ƫ��45�㷽���ϵ�B�����ο����ݣ�![]() ��1.732�������ȷ��0.1����
��1.732�������ȷ��0.1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֻ������������ε�ש�е�һ�֣��ܹ������������( )
A. �������B. ��������C. ���˱���D. ��ʮ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ƽ��������������ֱ�ߣ�
�پ����㣨0��2����ƽ����x���ֱ�ߣ�
��ֱ��y=2x��8��
�۾����㣨0��12����ƽ����ֱ��y=��2x��ֱ�ߣ�
���о����㣨5��2������������������ֱ�߹��У� ��
A.0��
B.1��
C.2��
D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0�����㣨��1��0���͵㣨0����3�����Ҷ����ڵ������ޣ���P=a+b+c����P��ȡֵ��Χ�ǣ�������
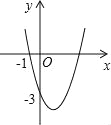
A. ��3��P����1 B. ��6��P��0 C. ��3��P��0 D. ��6��P����3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������һ��ȫ�ȵ���(����)
A. ����ȵ���������������
B. һ���Ƕ�Ӧ��ȵ���������������
C. б�߶�Ӧ��ȵ�����ֱ��������
D. �ױ���ȵ���������ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��5����b����8��������a��b��0����a��b��ֵΪ�� ��
A. 3 B. ��3 C. ��13 D. 13
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com