
【题目】如图,正方形![]() 的边长是3,
的边长是3,![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() ,并分别与边
,并分别与边![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,连接
,连接![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() .正确结论的个数为( )
.正确结论的个数为( )

A.1个B.2个C.3个D.4个
【答案】D
【解析】
由四边形ABCD是正方形,得到AD=BC=AB,∠DAB=∠ABC=90°,即可证明△DAP≌△ABQ,根据全等三角形的性质得到∠P=∠Q,根据余角的性质得到AQ⊥DP;故①正确;根据相似三角形的性质得到AO2=ODOP,故②正确;根据△CQF≌△BPE,得到S△CQF=S△BPE,根据△DAP≌△ABQ,得到S△DAP=S△ABQ,即可得到S△AOD=S四边形OECF;故③正确;根据相似三角形的性质得到BE的长,进而求得QE的长,证明△QOE∽△POA,根据相似三角形对应边成比例即可判断④正确,即可得到结论.
∵四边形ABCD是正方形,
∴AD=BC=AB,∠DAB=∠ABC=90°.
∵BP=CQ,
∴AP=BQ.
在△DAP与△ABQ中,∵ ,
,
∴△DAP≌△ABQ,
∴∠P=∠Q.
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP;
故①正确;
∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴![]() ,
,
∴AO2=ODOP.故②正确;
在△CQF与△BPE中,∵ ,
,
∴△CQF≌△BPE,
∴S△CQF=S△BPE.
∵△DAP≌△ABQ,
∴S△DAP=S△ABQ,
∴S△AOD=S四边形OECF;故③正确;
∵BP=1,AB=3,
∴AP=4.
∵∠P=∠P,∠EBP=∠DAP=90°,
∴△PBE∽△PAD,
∴![]() ,
,
∴BE![]() ,
,
∴QE![]() ,
,
∵∠Q=∠P,∠QOE=∠POA=90°,
∴△QOE∽△POA,
∴ ,
,
∴![]() ,故④正确.
,故④正确.
故选:D.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
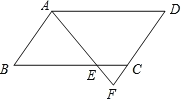
【题目】如图,在平行四边形ABCD中,点E在边BC上,射线AE交DC的延长线于点F,已知BE=3CE,△ABE的周长为9,则△ADF的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
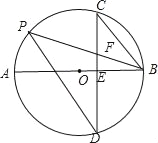
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,弦PB与CD交于点F,且FC=FB.
(1)求证:PD∥CB;
(2)若AB=26,EB=8,求CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有两个小岛![]() ,
,![]() ,某渔船在海中的
,某渔船在海中的![]() 处测得小岛D位于东北方向上,且相距
处测得小岛D位于东北方向上,且相距![]() ,该渔船自西向东航行一段时间到达点
,该渔船自西向东航行一段时间到达点![]() 处,此时测得小岛
处,此时测得小岛![]() 恰好在点
恰好在点![]() 的正北方向上,且相距
的正北方向上,且相距![]() ,又测得点
,又测得点![]() 与小岛
与小岛![]() 相距
相距![]() .
.
(1)求![]() 的值;
的值;
(2)求小岛![]() ,
,![]() 之间的距离(计算过程中的数据不取近似值).
之间的距离(计算过程中的数据不取近似值).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:

如图(1),在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.经过社团成员讨论发现:过点
的长.经过社团成员讨论发现:过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() 就可以解决问题,如图(2).请回答:
就可以解决问题,如图(2).请回答:![]() ______
______![]() .
.
(2)求![]() 的长.
的长.
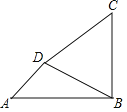
(3)请参考以上解决思路,解决问题:如图(3),在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
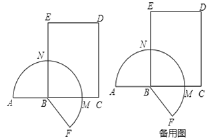
【题目】如图,点![]() 为长为5的线段
为长为5的线段![]() 上一点,且
上一点,且![]() ,过
,过![]() 作
作![]() 于
于![]() ,且
,且![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() ,将线段
,将线段![]() 绕点B顺时针旋转,得到线段
绕点B顺时针旋转,得到线段![]() ,优弧
,优弧![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,设旋转角为
,设旋转角为![]()
(1)若扇形![]() 的面积为
的面积为![]() ,则
,则![]() 的度数为_______.
的度数为_______.
(2)连接![]() ,判断
,判断![]() 与扇形
与扇形![]() 所在圆
所在圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(3)设![]() 为直线
为直线![]() 上一点,沿
上一点,沿![]() 所在直线折叠矩形,若折叠
所在直线折叠矩形,若折叠![]() 后所在的直线与扇形
后所在的直线与扇形![]() 所在
所在![]() 的相切,求
的相切,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
【答案】②③
【解析】分析:(1)根据题目中给的计算方法代入计算后判定即可;(2)根据题目中给的计算方法代入计算后判定即可;(3)根据题目中给的计算方法代入计算后判定即可;(4)结合x的取值范围,分类讨论,利用题目中给出的方法计算后判定即可.
详解:
①当x=1.7时,
[x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;
②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;
③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;
④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x=![]() ;x+1=4x时,得x=
;x+1=4x时,得x=![]() ;当x=0时,y=4x=0,
;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为:②③.
点睛:本题是阅读理解题,前三问比较容易判定,根据题目所给的方法判定即可;第四问较难,结合x的取值范围分情况讨论即可.
【题型】填空题
【结束】
19
【题目】先化简再求值: ![]() ,其中
,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com