
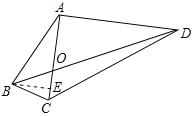
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:

如图(1),在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.经过社团成员讨论发现:过点
的长.经过社团成员讨论发现:过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() 就可以解决问题,如图(2).请回答:
就可以解决问题,如图(2).请回答:![]() ______
______![]() .
.
(2)求![]() 的长.
的长.
(3)请参考以上解决思路,解决问题:如图(3),在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)75°;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据平行线的性质可得出∠ADB=∠OAC=75°;
(2)结合∠BOD=∠COA可得出△BOD∽△COA,利用相似三角形的性质可求出OD的值,进而可得出AD的值,由三角形内角和定理可得出∠ABD=75°=∠ADB,由等角对等边可得出AB的长;
(3)过点B作BE∥AD交AC于点E,同(1)可得出AE的长.在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解.
(1)∵BD∥AC,
∴∠ADB=∠OAC=75°.
(2)∵∠BOD=∠COA,∠ADB=∠OAC,
∴△BOD∽△COA,
∴![]() .
.
又∵AO![]() ,
,
∴OD![]() AO
AO![]() ,
,
∴AD=AO+OD=![]() .
.
∵∠BAD=30°,∠ADB=75°,
∴∠ABD=180°﹣∠BAD﹣∠ADB=75°=∠ADB,
∴AB=AD=![]() .
.
(3)过点B作BE∥AD交AC于点E,如图所示.
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°.
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴![]() .
.
∵BO:OD=1:3,
∴![]() .
.
∵AO=![]() ,
,
∴EO![]() ,
,
∴AE=![]() .
.
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
∴AB=2BE.
在Rt△AEB中,BE2+AE2=AB2,即(![]() )2+BE2=(2BE)2,
)2+BE2=(2BE)2,
解得:BE=![]() ,
,
∴AB=AC=![]() ,AD=4.
,AD=4.
在Rt△CAD中,AC2+AD2=CD2,即![]() ,
,
解得:CD=![]() .
.


科目:初中数学 来源: 题型:
【题目】蜜蜂是自然界神奇的“建筑师”,它能用最少的材料造成最牢固的建筑物“蜂窝”,观察下列的“蜂窝图”.
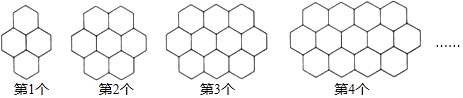
(1)若“![]() “中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有 个建筑单位:第3个图案中共有 个建筑单位;第n个图案中共有 个建筑单位.(用含有n的代数式表示)
“中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有 个建筑单位:第3个图案中共有 个建筑单位;第n个图案中共有 个建筑单位.(用含有n的代数式表示)
(2)若现在有74个建筑单位材料,能建成符合上述规律的“蜂窝”吗?若能求出它符合第几图形,若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经知道一些特殊的勾股数,如三连续正整数中的勾股数:3、4、5;三个连续的偶数中的勾股数6、8、10;事实上,勾股数的正整数倍仍然是勾股数.
(1)另外利用一些构成勾股数的公式也可以写出许多勾股数,毕达哥拉斯学派提出的公式:a=2n+1,b=2n2+2n,c=2n2+2n+1(n为正整数)是一组勾股数,请证明满足以上公式的a、b、c的数是一组勾股数.
(2)然而,世界上第一次给出的勾股数公式,收集在我国古代的着名数学着作《九章算术》中,书中提到:当a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
(m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长是3,
的边长是3,![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() ,并分别与边
,并分别与边![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,连接
,连接![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() .正确结论的个数为( )
.正确结论的个数为( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现任意三个连续的整数中,最大数与最小数这两个数的平方差是4的倍数;
验证:(1) ![]() 的结果是4的几倍?
的结果是4的几倍?
(2)设三个连续的整数中间的一个为n,计算最大数与最小数这两个数的平方差,并说明它是4的倍数;
延伸:说明任意三个连续的奇数中,最大的数与最小的数这两个数的平方差是8的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
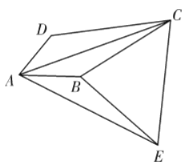
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,点
,点![]() 在四边形
在四边形![]() 内部运动,且满足
内部运动,且满足![]() ,求点
,求点![]() 运动路径的长度.
运动路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com