
【题目】蜜蜂是自然界神奇的“建筑师”,它能用最少的材料造成最牢固的建筑物“蜂窝”,观察下列的“蜂窝图”.
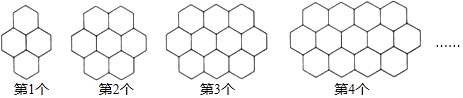
(1)若“![]() “中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有 个建筑单位:第3个图案中共有 个建筑单位;第n个图案中共有 个建筑单位.(用含有n的代数式表示)
“中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有 个建筑单位:第3个图案中共有 个建筑单位;第n个图案中共有 个建筑单位.(用含有n的代数式表示)
(2)若现在有74个建筑单位材料,能建成符合上述规律的“蜂窝”吗?若能求出它符合第几图形,若不能请说明理由.
【答案】(1)30;41;8+11n;(2)能建成符合上述规律的“蜂窝”,它符合第6图形.
【解析】
(1)第2个图案中共有19+11×1=30个建筑单位,第3个图案中共有19+11×2=41个建筑单位,据此分析即可得到第n个图案中共有![]() 个建筑单位;
个建筑单位;
(2)根据题意![]() ,解得
,解得![]() ,所以能建成符合上述规律的“蜂窝“,它符合第6图形.
,所以能建成符合上述规律的“蜂窝“,它符合第6图形.
(1)第1个图形中共有19个建筑单位,
第2个图案中共有19+11×1=30个建筑单位,
第3个图案中共有19+11×2=41个建筑单位,
![]()
第![]() 个图案中共有
个图案中共有![]() 个建筑单位,
个建筑单位,
故答案为:30,41,![]() ;
;
(2)能建成符合上述规律的“蜂窝“,它符合第6图形.
理由:根据题意: ![]() ,
,
解得:![]() ,
,
∴能建成符合上述规律的“蜂窝”,它符合第6图形.


科目:初中数学 来源: 题型:
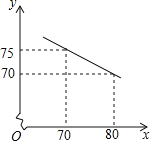
【题目】为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业,王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价x(元)和游客居住房间数y(间)的信息,乐乐绘制出y与x的函数图象如图所示:
(1)求y与x之间的函数关系式;
(2)合作社规定每个房间价格不低于60元且不超过150元,对于游客所居住的每个房间,合作社每天需支出20元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
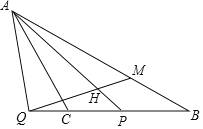
【题目】如图,已知等腰△ABC,∠ACB=120°,P是线段CB上一动点(与点C,B不重合),连接AP,延长BC至点Q,使得∠PAC=∠QAC,过点Q作射线QH交线段AP于H,交AB于点M,使得∠AHQ=60°.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示);
(2)用等式表示线段QC和BM之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级举行了“中国梦”演讲比赛活动,学校团委根据学生的成绩划分为A,B,C,D四个等级,并绘制了如下两个不完整的两种统计图.
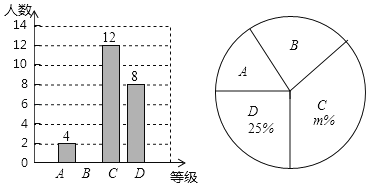
根据图中提供的信息,回答下列问题
(1)参加演讲比赛的学生共有 人,并把条形图补充完整;
(2)扇形统计图中,m= ;C等级对应的扇形的圆心角为 度.
(3)学校准备从获得A等级的学生中随机选取2人,参加全市举办的演讲比赛,请利用列表法或树状图法,求获得A等级的小明参加市比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙二人走步晨练,两人同时同地向距离600米的目标出发,二人所走的路程y(米)与所走的时间t(分)之间的函数关系如图所示,下列说法:①甲走全程的平均速度为75米/分:②第4分钟时,二人在途中相遇;③第2分钟时甲在乙前面100米处;④乙比甲提前2.5分钟到达终点;其中正确的有( )个.
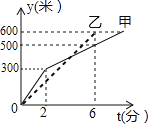
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
A 类 | 50 | 25 |
B 类 | 200 | 20 |
C 类 | 400 | 15 |
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为( )
A.购买A类会员卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017山东省菏泽市,第20题,7分)如图,一次函数y=kx+b与反比例函数![]() 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:

如图(1),在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.经过社团成员讨论发现:过点
的长.经过社团成员讨论发现:过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() 就可以解决问题,如图(2).请回答:
就可以解决问题,如图(2).请回答:![]() ______
______![]() .
.
(2)求![]() 的长.
的长.
(3)请参考以上解决思路,解决问题:如图(3),在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com