
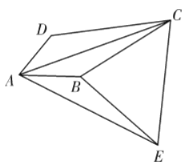
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,点
,点![]() 在四边形
在四边形![]() 内部运动,且满足
内部运动,且满足![]() ,求点
,求点![]() 运动路径的长度.
运动路径的长度.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)根据等式的基本性质可得![]() ,然后利用SAS即可证出
,然后利用SAS即可证出![]() ≌
≌![]() ;
;
(2)根据四边形的内角和和全等三角形的性质可得![]() ,从而求出∠CBE=90°,根据勾股定理可得
,从而求出∠CBE=90°,根据勾股定理可得![]() ,根据等边三角形的判定及性质可得
,根据等边三角形的判定及性质可得![]() ,从而证出结论;
,从而证出结论;
(3)如图,设![]() 为满足条件的点,将
为满足条件的点,将![]() 绕着点
绕着点![]() 顺时针旋转60度得
顺时针旋转60度得![]() ,连接
,连接![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() , DB,先利用SAS证出
, DB,先利用SAS证出![]() ≌
≌![]() ,从而得出
,从而得出![]() ,∠AQD=∠AFB,然后证出
,∠AQD=∠AFB,然后证出![]() 为等边三角形,△ADB为等边三角形,从而得出
为等边三角形,△ADB为等边三角形,从而得出![]() , DB=AB=2,然后根据勾股定理的逆定理可得
, DB=AB=2,然后根据勾股定理的逆定理可得![]() ,根据四点共圆证出点
,根据四点共圆证出点![]() 的路径为过
的路径为过![]() 、
、![]() 、
、![]() 三点的圆上
三点的圆上![]() ,求出圆心角和半径即可求出点
,求出圆心角和半径即可求出点![]() 运动路径的长度.
运动路径的长度.
证明:(1)∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
∴![]() ≌
≌![]()
(2)在四边形![]() 中
中
![]()
∵![]() ≌
≌![]()
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
又∵![]() ,
,![]()
∴△AEC为等边三角形
∴![]()
∴![]()
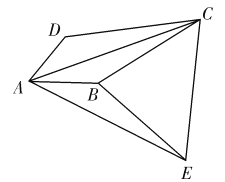
(3)如图,设![]() 为满足条件的点,将
为满足条件的点,将![]() 绕着点
绕着点![]() 顺时针旋转60度得
顺时针旋转60度得![]() ,连接
,连接![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() , DB.
, DB.

∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
∴![]() ≌
≌![]()
∴![]() ,∠AQD=∠AFB,
,∠AQD=∠AFB,
∵![]() ,AQ=AF,∠DAB=60°,AD=AB
,AQ=AF,∠DAB=60°,AD=AB
∴![]() 为等边三角形,△ADB为等边三角形
为等边三角形,△ADB为等边三角形
∴![]() , DB=AB=2
, DB=AB=2
∵![]()
∴![]()
∴![]()
∴![]()
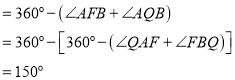
∵∠BCD=30°
∴∠DQB+∠BCD=180°
∴点![]() 的路径为过
的路径为过![]() 、
、![]() 、
、![]() 三点的圆上
三点的圆上![]()
设圆心为![]() ,连接OD、OB
,连接OD、OB
则![]() ,
,
∴△OBD为等边三角形
∴![]() ,
,
∴点![]() 的运动的路径长为:
的运动的路径长为:![]() .
.


科目:初中数学 来源: 题型:
【题目】一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
A 类 | 50 | 25 |
B 类 | 200 | 20 |
C 类 | 400 | 15 |
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为( )
A.购买A类会员卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,弦PB与CD交于点F,且FC=FB.
(1)求证:PD∥CB;
(2)若AB=26,EB=8,求CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:

如图(1),在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.经过社团成员讨论发现:过点
的长.经过社团成员讨论发现:过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() 就可以解决问题,如图(2).请回答:
就可以解决问题,如图(2).请回答:![]() ______
______![]() .
.
(2)求![]() 的长.
的长.
(3)请参考以上解决思路,解决问题:如图(3),在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
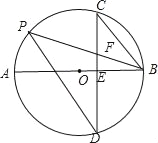
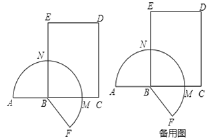
【题目】如图,点![]() 为长为5的线段
为长为5的线段![]() 上一点,且
上一点,且![]() ,过
,过![]() 作
作![]() 于
于![]() ,且
,且![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() ,将线段
,将线段![]() 绕点B顺时针旋转,得到线段
绕点B顺时针旋转,得到线段![]() ,优弧
,优弧![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,设旋转角为
,设旋转角为![]()
(1)若扇形![]() 的面积为
的面积为![]() ,则
,则![]() 的度数为_______.
的度数为_______.
(2)连接![]() ,判断
,判断![]() 与扇形
与扇形![]() 所在圆
所在圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(3)设![]() 为直线
为直线![]() 上一点,沿
上一点,沿![]() 所在直线折叠矩形,若折叠
所在直线折叠矩形,若折叠![]() 后所在的直线与扇形
后所在的直线与扇形![]() 所在
所在![]() 的相切,求
的相切,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
【答案】②③
【解析】分析:(1)根据题目中给的计算方法代入计算后判定即可;(2)根据题目中给的计算方法代入计算后判定即可;(3)根据题目中给的计算方法代入计算后判定即可;(4)结合x的取值范围,分类讨论,利用题目中给出的方法计算后判定即可.
详解:
①当x=1.7时,
[x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;
②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;
③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;
④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x=![]() ;x+1=4x时,得x=
;x+1=4x时,得x=![]() ;当x=0时,y=4x=0,
;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为:②③.
点睛:本题是阅读理解题,前三问比较容易判定,根据题目所给的方法判定即可;第四问较难,结合x的取值范围分情况讨论即可.
【题型】填空题
【结束】
19
【题目】先化简再求值: ![]() ,其中
,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月5日,第二届中国国际进口博览会(The 2nd China International lmport Expo)在上海国家会展中心开幕.本次进博会将共建开放合作、创新共享的世界经济,见证海纳百川的中国胸襟,诠释兼济天下的责任担当.小滕、小刘两人想到四个国家馆参观:![]() .中国馆;
.中国馆;![]() .俄罗斯馆;
.俄罗斯馆;![]() .法国馆;
.法国馆;![]() .沙特阿拉伯馆.他们各自在这四个国家馆中任意选择一个参观,每个国家馆被选择的可能性相同.
.沙特阿拉伯馆.他们各自在这四个国家馆中任意选择一个参观,每个国家馆被选择的可能性相同.
(1)求小滕选择![]() .中国馆的概率;
.中国馆的概率;
(2)用画树状图或列表的方法,求小滕和小刘恰好选择同一国家馆的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM、PN、MN,则下列结论:①PM=PN;②![]() ;③若∠ABC=60°,则△PMN为等边三角形;④若∠ABC=45°,则BN=
;③若∠ABC=60°,则△PMN为等边三角形;④若∠ABC=45°,则BN=![]() PC.其中正确的是( )
PC.其中正确的是( )
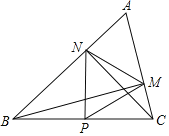
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com