
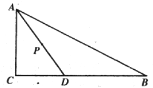
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() .点
.点![]() 是线段
是线段![]() 上一动点,当半径为
上一动点,当半径为![]() 的
的![]() 与
与![]() 的一边相切时,
的一边相切时,![]() 的长为____________.
的长为____________.
【答案】![]() 或
或![]() 或
或![]()
【解析】
根据勾股定理得到AB、AD的值,再分3种情况根据相似三角形性质来求AP的值.
解:∵在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴AD=![]()
在Rt△ACB中,![]() ,
,![]() ,
,![]() ,
,![]()
∴CB=6+10=16
∵AB =AC +BC
AB=![]()
①当⊙P与BC相切时,设切点为E,连结PE, 则PE=4,∠AEP=90°
∵AD=BD=10
∴∠EAP=∠CBA, ∠C=∠AEP=90°
∴△APE∽△ACB
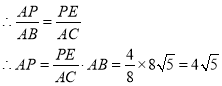
②当⊙P与AC相切时,设切点为F,连结PF,则PF=4,∠AFP=90°
∵∠C=∠AFP=90°
∠CAD=∠FAP
∴△CAD∽△FAP
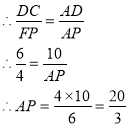
③当⊙P与BC相切时,设切点为G,连结PG,则PG=4,∠AGP=90°
∵∠C=∠PGD=90°
∠ADC=∠PDG
∴△CAD∽△GPD
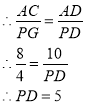
故答案为:![]() 或
或![]() 或5
或5


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
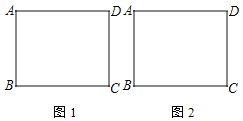
【题目】已知矩形ABCD,其中AD>AB,依题意先画出图形,然后解答问题.
(1)F为DC边上一点,把△ADF沿AF折叠,使点D恰好落在BC上的点E处.在图1中先画出点E,再画出点F,若AB=8,AD=10,直接写出EF的长为 ;
(2)把△ADC沿对角线AC折叠,点D落在点E处,在图2先画出点E,AE交CB于点F,连接BE.求证:△BEF是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现任意三个连续的整数中,最大数与最小数这两个数的平方差是4的倍数;
验证:(1) ![]() 的结果是4的几倍?
的结果是4的几倍?
(2)设三个连续的整数中间的一个为n,计算最大数与最小数这两个数的平方差,并说明它是4的倍数;
延伸:说明任意三个连续的奇数中,最大的数与最小的数这两个数的平方差是8的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
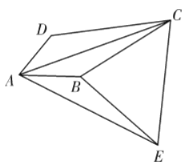
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,点
,点![]() 在四边形
在四边形![]() 内部运动,且满足
内部运动,且满足![]() ,求点
,求点![]() 运动路径的长度.
运动路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
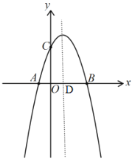
【题目】如图,二次函数![]() 的图象与x轴交于A,B两点,与y轴交于点C,对称轴与x轴交于点D,若点P为y轴上的一个动点,连接PD,则
的图象与x轴交于A,B两点,与y轴交于点C,对称轴与x轴交于点D,若点P为y轴上的一个动点,连接PD,则![]() 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家所在居民楼的对面有一座大厦AB,高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
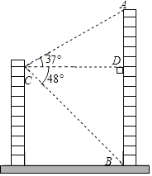
(1)求∠ACB的度数;
(2)求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com