
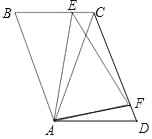
【题目】如图,在平行四边形ABCD中,AC=CD,若点E、F分别为边BC、CD上的两点,且∠EAF=∠CAD.
(1)求证:△ADF∽△ACE;
(2)求证:AE=EF.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据平行四边形的性质可得到∠BCA=∠CAB,由等边对等角可得到∠CAD=∠D,根据平行四边形的性质利用SAS可判定△BCA≌△DAC,由全等三角形的性质即可得到∠D=∠ACB,再根据相似三角形的判定得出即可;
(2)由△ADF∽△ACE可得到对应边成比例,已知∠EAF=∠CAD从而可推出△AEF∽△ACD,已知AC=CD,根据对应成比例不难得到结论.
解:(1)∵AC=CD,
∴∠D=∠CAD.
∵平行四边形ABCD,
∴AD∥BC,
∴∠CAD=∠ACB,
∴∠D=∠ACB.
∵∠EAF=∠CAD,
∴∠DAF=∠CAE,
∴△ADF∽△ACE;
(2)∵△ADF∽△ACE,
∴![]() ,
,
∵∠EAF=∠CAD,
∴△AEF∽△ACD,
∴![]() ,
,
又∵AC=CD,
∴AE=EF.


科目:初中数学 来源: 题型:
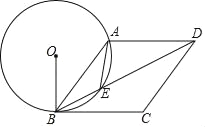
【题目】如图,点E在菱形ABCD的对角线BD上,连接AE,且AE=BE,⊙O是△ABE的外接圆,连接OB.
(1)求证:OB⊥BC;
(2)若BD=![]() ,tan∠OBD=2,求⊙O的半径.
,tan∠OBD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E,F,G分别是等边三角形ABC三边AB,BC,CA上的动点,且始终保持AE=BF=CG,设△EFG的面积为y,AE的长为x,y关于x的函数图象大致为图2所示,则等边三角形ABC的边长为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
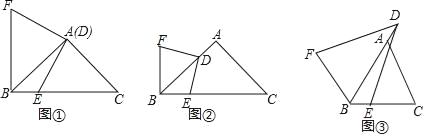
【题目】观察猜想:(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是 ,BE+BF= ;
探究证明:(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;
拓展延伸:(3)如图③,在△ABC中,AB=AC,∠BAC=a,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=a,连接BF,则BE+BF的值是多少?请用含有n,a的式子直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
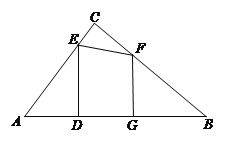
(1)当AD=3时,求DE的长;
(2)当点E、F在边AC、BC上移动时,设![]() ,求y关于x的函数解析式,并写出函数的定义域;
,求y关于x的函数解析式,并写出函数的定义域;
(3) 在点E、F移动过程中,△AED与△CEF能否相似,若能,求AD的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 图1是一款优雅且稳定的抛物线型落地灯.防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为_____米.
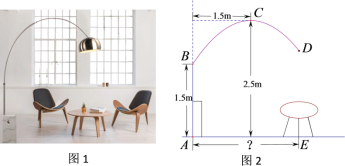
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.
(1)求证:△CAB∽△EPB;
(2)若AB=10,AC=6,BP=5,求CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O是边长为2的正方形ABCD的中心.函数y=(x﹣h)2的图象与正方形ABCD有公共点,则h的取值范围是_____.
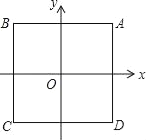
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com