练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知△ABC∽△DEF，面积比为9：4，则△ABC与△DEF的对应边之比为（ ）

    A. 3：4B. 3：2C. 9：16D. 2：3

    【答案】B

    【解析】

    根据相似三角形的面积比等于相似比的平方即可求解．

    解：∵△ABC∽△DEF，面积比为9：4，

    ∴△ABC与△DEF的对应边之比3：2．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．
    （1）求证：∠ADB=∠CDB；
    （2）若∠ADC=90°，求证：四边形MPND是正方形．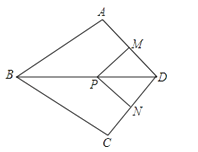

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一张长方形纸片与一张直角三角形纸片(∠EFG＝90°)按如图所示的位置摆放，
    使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上，已知∠BEF＝21°，则
    ∠CMF＝ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在纪念中国抗日战争胜利70周年之际，某公司决定组织员工观看抗日战争题材的影片，门票有甲乙两种，甲种票比乙种票每张贵6元；买甲种票10张，乙种票15张共用去660元．

    （1）求甲、乙两种门票每张各多少元？

    （2）如果公司准备购买35张门票且购票费用不超过1000元，那么最多可购买多少张甲种票？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点P（2，﹣3）关于原点对称的点的坐标是（ ）
    A.（﹣2，﹣3）
    B.（2，3）
    C.（﹣2，3）
    D.（﹣3，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】实验探究：
    （1）动手操作：
    ①如图1，将一块直角三角板DEF放置在直角三角板ABC上，使三角板DEF的两条直角边DE、DF分别经过点B、C，且BC∥EF，已知∠A=30°，则∠ABD+∠ACD=；
    ②如图2，若直角三角板ABC不动，改变等腰直角三角板DEF的位置，使三角板DEF的两条直角边DE、DF仍然分别经过点B、C，那么∠ABD+∠ACD=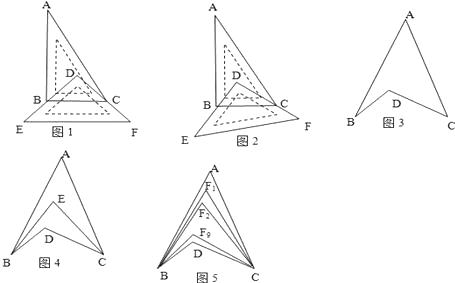
    （2）猜想证明：
    如图3，∠BDC与∠A、∠B、∠C之间存在着什么关系，并说明理由；
    （3）灵活应用：
    请你直接利用以上结论，解决以下列问题：
    ①如图4，BE平分∠ABD，CE平分∠ACB，若∠BAC=40°，∠BDC=120°，求∠BEC的度数；
    （4）②如图5，∠ABD，∠ACD的10等分线相交于点F1、F2、…、F9 ，
    若∠BDC=120°，∠BF3C=64°，则∠A的度数为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．

    （1）探究猜想：
    ①若∠A=20°，∠D=40°，则∠AED=
    ②猜想图①中∠AED，∠EAB，∠EDC的关系，并用两种不同的方法证明你的结论．
    （2）拓展应用：
    如图②，射线FE与l1 ， l2交于分别交于点E、F，AB∥CD，a，b，c，d分别是被射线FE隔开的4个区域（不含边界，其中区域a，b位于直线AB上方，P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF的关系（任写出两种，可直接写答案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若3am+2b4与﹣a5bn﹣1的和仍是一个单项式，则m+n= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D，E分别是AB，AC的中点，∠A=50°，∠ADE=60°，则∠C的度数为（ ）

    A.50°
    B.60°
    C.70°
    D.80°

    查看答案和解析>>

    同步练习册答案