练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知经过原点的直线与反比例函数图象分别相交于点和点，过点作轴于点，若的面积为，则的值为（ ）

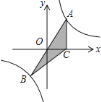
    A. 2 B. 4 C. 6 D. 8

    【答案】B

    【解析】

    首先根据反比例函数与正比例函数的图象特征，可知A、B两点关于原点对称，则O为线段AB的中点，故△BOC的面积等于△AOC的面积，都等于2，然后由反比例函数y=的比例系数k的几何意义，可知△AOC的面积等于|k|，从而求出k的值．

    解：∵反比例函数与正比例函数的图象相交于A、B两点，

    ∴A、B两点关于原点对称，

    ∴OA=OB，

    ∴△BOC的面积=△AOC的面积=4÷2=2，

    又∵A是反比例函数y=图象上的点，且AC⊥x轴于点C，

    ∴△AOC的面积=|k|，

    ∴|k|=2，

    ∵k＞0，

    ∴k=4．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】观察下列方程及其解的特征：

    （1）的解为；

    （2）的解为，；

    （3）的解为，；

    解答下列问题：

    请猜想：方程的解为________；

    请猜想：关于的方程________的解为，；

    下面以解方程为例，验证中猜想结论的正确性．

    解：原方程可化为．

    （下面请大家用配方法写出解此方程的详细过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线MN经过正方形ABCD的顶点D且不与正方形的任何一边相交，AM⊥MN于M，CN⊥MN于N，BR⊥MN于R。

    (1)求证：△ADM≌△DCN

    (2)求证：MN=AM+CN

    (3)试猜想BR与MN的数量关系，并证明你的猜想

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，已知在直角梯形OABC中，AB∥OC，BC⊥x轴于点C、A（1，1）、B（3，1）．动点P从O点出发，沿x轴正方向以每秒1个单位长度的速度移动．过P点作PQ垂直于直线OA，垂足为Q．设P点移动的时间为t秒（0＜t＜4），△OPQ与直角梯形OABC重叠部分的面积为S．

    （1）求经过O、A、B三点的抛物线解析式；

    （2）求S与t的函数关系式；

    （3）将△OPQ绕着点P顺时针旋转90°，是否存在t，使得△OPQ的顶点O或Q在抛物线上？若存在，直接写出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)方法感悟：如图①，在正方形ABCD中，点E、F分别为DC、BC边上的点，且满足∠EAF=45°，连接EF．将△ADE绕点A顺时针旋转90°得到△ABG，易证△GAF≌△EAF，从而得到结论：DE+BF=EF．根据这个结论，若CD＝6，DE＝2，求EF的长．

    （2）方法迁移：如图②，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且∠EAF=∠BAD，试猜想DE，BF，EF之间有何数量关系，证明你的结论．

    （3）问题拓展：如图③，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E、F分别是边BC、CD延长线上的点，且∠EAF=∠BAD，试探究线段EF、BE、FD之间的数量关系，请直接写出你的猜想（不必说明理由）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是某同学对多项式（x2﹣4x+2）（x2﹣4x+6）+4进行因式分解的过程

    解：设x2﹣4x＝y，

    原式＝（y+2）（y+6）+4　（第一步）

    ＝y2+8y+16　（第二步）

    ＝（y+4）2（第三步）

    ＝（x2﹣4x+4）2（第四步）

    （1）该同学第二步到第三步运用了因式分解的　 　（填序号）．

    A．提取公因式 B．平方差公式

    C．两数和的完全平方公式 D．两数差的完全平方公式

    （2）该同学在第四步将y用所设中的x的代数式代换，得到因式分解的最后结果．这个结果是否分解到最后？　 　．（填“是”或“否”）如果否，直接写出最后的结果　 　．

    （3）请你模仿以上方法尝试对多项式（x2﹣2x）（x2﹣2x+2）+1进行因式分解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲汽车出租公司按每100千米150元收取租车费：乙汽车出租公司按每100千米50元收取租车费，另加管理费800元设用车里程为x千米租用甲、乙两家公司的汽车费用分别为元、元

    分别求出、与x之间的函数关系式；

    判断x在什么范围内，租用乙公司的汽车费用比租用甲公司的汽车费用少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4800元．已知甲、乙两车单独运完此堆垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元．

    （1）求甲、乙两车单独运完此堆垃圾各需运多少趟？

    （2）若单独租用一台车，租用哪台车合算？

    查看答案和解析>>

    同步练习册答案