
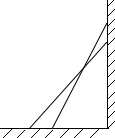
 如图,一架云梯长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.
如图,一架云梯长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.分析 (1)由题意得a=24米,c=25米,根据勾股定理a2+b2=c2,可求出梯子底端离墙有多远.
(2)由题意得此时y=20米,c=25米,由勾股定理可得出此时的x,继而能和(1)的b进行比较.
解答  解:(1)由题意得此时a=24米,c=25米,根据a2+b2=c2,
解:(1)由题意得此时a=24米,c=25米,根据a2+b2=c2,
可得:b=7米,
答:这个梯子底端离墙有7米;
(2)不是.
理由:设滑动后梯子的底端到墙的距离为x米,
得方程,x2+(24-4)2=252,
解得:x=15,
所以梯子向后滑动了8米.
综合得:如果梯子的顶端下滑了4米,那么梯子的底部在水平方向不是滑4米.
点评 本题考查了勾股定理的应用,熟悉勾股定理,能从实际问题中抽象出勾股定理是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
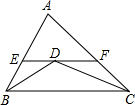 如图,△ABC中,∠ABC、∠ACB的平分线相交于点D,过D作直线平行于BC,交AB、AC于E、F,若BE+CF=7.则EF=( )
如图,△ABC中,∠ABC、∠ACB的平分线相交于点D,过D作直线平行于BC,交AB、AC于E、F,若BE+CF=7.则EF=( )| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+3)2=-4 | B. | (x-3)2=4 | C. | (x+3)2=5 | D. | (x+3)2=±$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
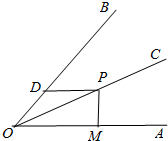 如图,OC平分∠AOB,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=3,则PD的长为( )
如图,OC平分∠AOB,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=3,则PD的长为( )| A. | 2 | B. | 1.5 | C. | 3 | D. | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
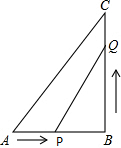 如图所示,在Rt△ABC中.∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
如图所示,在Rt△ABC中.∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com