
| A. | (x+3)2=-4 | B. | (x-3)2=4 | C. | (x+3)2=5 | D. | (x+3)2=±$\sqrt{5}$ |
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
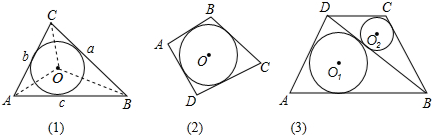
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 |
| 人数 | a | -100 | +550 | -200 | +600 | -300 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
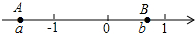
| A. | a+b<0 | B. | a-b>0 | C. | ab>0 | D. | $\frac{a}{b}$>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
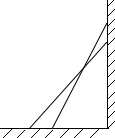 如图,一架云梯长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.
如图,一架云梯长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
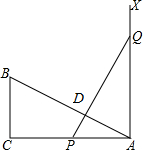 如图,有一个直角三角形ABC,∠C=90°,AB=8,BC=3,P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动,PQ交AB于点D,且PQ=AB.问当AD=4时,才能使△ABC≌△PQA.
如图,有一个直角三角形ABC,∠C=90°,AB=8,BC=3,P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动,PQ交AB于点D,且PQ=AB.问当AD=4时,才能使△ABC≌△PQA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com