练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知函数y=（m+1）x|2m|﹣1 ，

    ①当m何值时，y是x的正比例函数？②当m何值时，y是x的反比例函数？

    （上述两个问均要求写出解析式）

    【答案】①当m=1时，y是x的正比例函数；②当m=0时，y是x的反比例函数

    【解析】

    ①根据正比例函数的定义得到|2m|-1=1，且m+1≠0，由此即可求得答案；

    ②根据反比例函数的定义得到|2m|-1=-1，且m+1≠0，由此即可求得.

    ①∵函数y=（m+1）x|2m|﹣1是正比例函数，

    ∴|2m|﹣1=1，且m+1≠0，

    解得，m=1，

    即当m=1时，y=2x，y是x的正比例函数；

    ②∵函数y=（m+1）x|2m|﹣1是反比例函数，

    ∴|2m|﹣1=﹣1，且m+1≠0，

    解得，m=0；

    即当m=0时，y=，y是x的反比例函数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，边长为1的正方形ABCD的对角线AC，BD相交于点O，直角∠MPN的顶点P与点O重合，直角边PM，PN分别与OA，OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是_____.

    （1）EF=OE；（2）S四边形OEBF：S正方形ABCD=1：4；（3）在旋转过程中，当△BEF与△COF的面积之和最大时，AE=；（4）OGBD=AE2+CF2.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线 （a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：

    ①4ac＜b2；

    ②方程 的两个根是x1=﹣1，x2=3；

    ③3a+c＞0

    ④当y＞0时，x的取值范围是﹣1≤x＜3

    ⑤当x＜0时，y随x增大而增大

    其中结论正确的个数是（　　）

    A. 4个 B. 3个 C. 2个 D. 1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC是相似三角形，求AP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

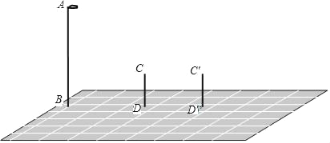
    【题目】如图，AB表示路灯，CD、C′D′表示小明所在两个不同位置：

    （1）分别画出这两个不同位置小明的影子；

    （2）小明发现在这两个不同的位置上，他的影子长分别是自己身高的1倍和2倍，他又量得自己的身高为1.5米，DD′长为3米，你能帮他算出路灯的高度吗？（B、D、D′在一条直线上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，双曲线（x＞0）上有一点A（1，5），过点A的直线y=mx+n与x轴交于点C（6，0）．

    （1）求反比例函数和一次函数的解析式；

    （2）连接OA、OB，求△AOB的面积；

    （3）根据图象直接写出在第一象限内反比例函数值大于一次函数值时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

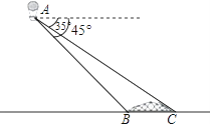
    【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC，并测得B、C两点的俯角分别为45°、35°．已知大桥BC与地面在同一水平面上，其长度为100m，求热气球离地面的高度．（结果保留整数）（参考数据：sin35°=0.57，cos35°=0.82，tan35°=0.70）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

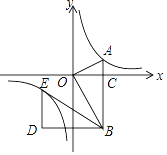
    【题目】如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（，1）在反比例函数y=的图象上．

    （1）求k的值；

    （2）若将△BOA绕点B按逆时针方向旋转60°，得到△BDE，判断点E是否在该反比例函数的图象上，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电视台“中国梦”栏目的一位记者乘汽车赴360km外的农村采访，全程的前一部分为高速公路，后一部分为乡村公路．若汽车在高速公路和乡村公路上分别以某一速度匀速行驶，汽车行驶的路程y（单位：km）与时间x（单位：h）之间的关系如图所示，则下列结论正确的是_____（填序号）．

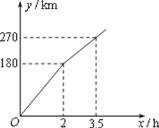
    （1）汽车在高速公路上的行驶速度为100km/h

    （2）乡村公路总长为90km

    （3）汽车在乡村公路上的行驶速度为60km/h

    （4）该记者在出发后5h到达采访地．

    查看答案和解析>>

    同步练习册答案