
【题目】(如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点 M处,点C落在点N处,MN与CD交于点P, 连接EP.
⑴如图②,若M为AD边的中点,①△AEM的周长=_________cm;②求证:EP=AE+DP;
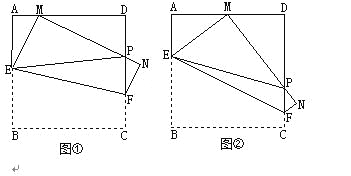
⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.
【答案】(1)①6 ②见解析(2)△PDM的周长保持不变,理由见解析
【解析】
(1)①由折叠知BE=EM,AE+EM+AM=AE+EB+AM=AB+AM,根据边长及中点易求周长;②取EP中点G,连接MG,再根据梯形中位线与三角形中位线解答即可;(2)不变化,可证△AEM∽△DMP,两个三角形的周长比为AE:MD,设AM=x,根据勾股定理可以用x表示MD的长与△MAE的周长,再根据周长比等于相似比,即可求解.
(1)①由折叠可知,BE=BM,∠B=∠MEP=90°,
△AEM的周长= AE+EM+AM=AE+EB+AM=AB+AM.
∵AB=4,M是AD中点,
∴△AEM的周长=6(cm)
②证明:取EP中点G,连接MG,在梯形AEPD中
∵M、G分别为AD、EP的中点
∴![]()
由折叠,得∠EMP=∠B=90°
又G为EP的中点
∴MG=![]() EP
EP
∴EP="AE+DP"

(2)△PDM的周长保持不变
证明:设AM=xcm,则DM=(4-x)cm
Rt△EAM中,由![]()
![]()
∵∠AME+∠AEM=90°
∠AME+∠PMD=90°
∴∠AEM=∠PMD
又∵∠A=∠D=90°
∴△PDM∽△MAE
∴![]()
即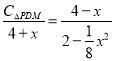
∴
∴△PDM的周长保持不变.


科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线F:y=x2+bx+c的图象经过坐标原点O,且与x轴另一交点为(![]() ,0).
,0).

(1)求抛物线F的解析式;
(2)如图1,直线l:y![]() x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);
x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);
(3)在(2)中,若m![]() ,设点A′是点A关于原点O的对称点,如图2.
,设点A′是点A关于原点O的对称点,如图2.
①判断△AA′B的形状,并说明理由;
②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2+bx+c经过点(1,0),(0,
x2+bx+c经过点(1,0),(0,![]() ).
).
(1)求该抛物线的函数表达式;
(2)将抛物线y=﹣![]() x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
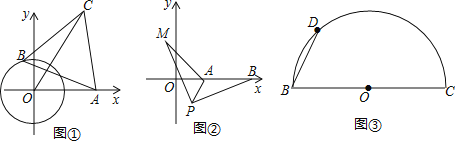
【题目】(发现问题)爱好数学的小明在做作业时碰到这样的一道题目:
如图①,点O为坐标原点,⊙O的半径为1,点A(2,0).动点B在⊙O上,连结AB,作等边△ABC(A,B,C为顺时针顺序),求OC的最大值
(解决问题)小明经过多次的尝试与探索,终于得到解题思路:在图①中,连接OB,以OB为边在OB的左侧作等边三角形BOE,连接AE.
(1)请你找出图中与OC相等的线段,并说明理由;
(2)求线段OC的最大值.
(灵活运用)
(3)如图②,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
(迁移拓展)
(4)如图③,BC=4![]() ,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.
,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动画片《小猪佩奇》分靡全球,受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.
(1)姐姐从中随机抽取一张卡片,恰好抽到A佩奇的概率为 ;
(2)若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四张背面完全相同的纸牌的正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀后摸出一张,不放回,再摸出一张
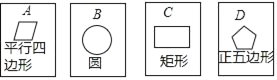
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出的两张纸牌牌面上所画几何图形既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com