
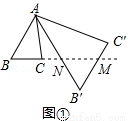
(本题满分10分)将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,如图①,我们将这种变换记为[θ,n].

(1)如图①,对△ABC作变换[50°, ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线BC′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线BC′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ 和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ 和n的值.
(1)5,50;(2)60°,2;(3)72°, .
.
【解析】
试题分析:(1)由旋转与相似的性质,即可得S△AB′C′:S△ABC=3,然后由△ABN与△B′MN中,∠B=∠B′,∠ANB=∠B′NM,可得∠BMB′=∠BAB′,即可求得直线BC与直线B′C′所夹的锐角的度数;
(2)由四边形 ABB′C′是矩形,可得∠BAC′=90°,然后由θ=∠CAC′=∠BAC′﹣∠BAC,即可求得θ的度数,又由含30°角的直角三角形的性质,即可求得n的值;
(3)由四边形ABB′C′是平行四边形,易求得θ=∠CAC′=∠ACB=72°,又由△ABC∽△B′BA,根据相似三角形的对应边成比例,易得AB2=CB•BB′=CB(BC+CB′),继而求得答案.
试题解析:(1)根据题意得:△ABC∽△AB′C′,∴S△AB′C′:S△ABC=( )2=5,∠B=∠B′,
)2=5,∠B=∠B′,
∵∠ANB=∠B′NM,∴∠BMB′=∠BAB′=50°;故答案为:5,50.
(2)∵四边形 ABB′C′是矩形,∴∠BAC′=90°.∴θ=∠CAC′=∠BAC′﹣∠BAC=90°—30°=60°.
在 Rt△ABC 中,∠ABB'=90°,∠BAB′=60°,∴∠AB′B=30°,∴n=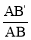 =2.
=2.
(3)∵四边形ABB′C′是平行四边形,∴AC′∥BB′,
又∵∠BAC=36°,∴θ=∠CAC′=∠ACB=72°.∴∠C′AB′=∠BAC=36°,而∠B=∠B,∴△ABC∽△B′BA,∴AB:BB′=CB:AB,∴AB2=CB•BB′=CB(BC+CB′),
而 CB′=AC=AB=B′C′,BC=1,∴AB2=1(1+AB),∴AB=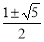 .∵AB>0,∴n=
.∵AB>0,∴n=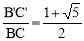 .
.
考点:1.相似三角形的判定与性质;2.平行四边形的性质;3.矩形的性质;4.旋转的性质.


科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
三角形的两边长分别为3和6,第三边的长是方程 的一个根,则这个三角形的周长为( )
的一个根,则这个三角形的周长为( )
A.11 B.13 C.11或 13 D.12
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市八年级上学期期中考试数学试卷(解析版) 题型:选择题
等腰三角形的一个角等于70o,则它的底角是( )
A. 70o B.55o C.60o D.70o或55o
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市滨湖区九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分6分)如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).

(1)以O为位似中心,作 ∽
∽ ,相似比为1:2,且保证
,相似比为1:2,且保证 在第三象限;
在第三象限;
(2)点 的坐标为( , );
的坐标为( , );
(3)若线段BC上有一点D,它的坐标为( ),那么它的对应点
),那么它的对应点 的坐标为( , ).
的坐标为( , ).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市滨湖区九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,MA、MB是⊙O的切线,切点分别为A、B,若∠ACB=65°,则∠AMB =_____.°

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期高效课堂调研数学试卷(解析版) 题型:解答题
(本题满分10分)如图,点A的坐标为(0,-4),点B为x轴上一动点,以线段AB为边作正方形ABCD(按逆时针方向标记),正方形ABCD随着点B的运动而相应变动.点E为y轴的正半轴与正方形ABCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m.

(1)当t=3时,求点C的坐标;
(2)当t>0时,求m与t之间的函数关系式;
(3)是否存在t,使点M(-2,2)落在正方形ABCD的边上?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:填空题
已知⊙O的半径为4cm,且线段OA的长为6cm,则线段OA的中点P在⊙O .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com