
【题目】(1)如图1,Rt△ABC中,若AC=4,BC=3,DE⊥AC,且DE=DB,求AD的长;
(2)如图2,已知△ABC,若AB边上存在一点M,若AC边上存在一点N,使MB=MN,且△AMN∽△ABC,请利用没有刻度的直尺和圆规,作出符合条件的线段MN(注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注).
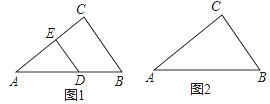
科目:初中数学 来源: 题型:
【题目】作图:
(1)如图1,△ABC在边长为1的正方形网格中:
①画出△ABC关于直线l轴对称的△DEF(其中D、E、F分别是A、B、C的对应点);
②直接写出△ABC中AB边上的高= .
(2)如图2,在四边形ABCD内找一点P,使得点P到AB、AD的距离相等,并且点P到点B、C的距离也相等.(用直尺与圆规作图,不写作法,保留作图痕迹).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校八年级某班举行演讲比赛,决定购买![]() ,
,![]() 两种笔记本作为奖品,已知
两种笔记本作为奖品,已知![]() ,
,![]() 两种笔记本的单价分别是
两种笔记本的单价分别是![]() 元和
元和![]() 元.根据比赛设奖情况,需购买笔记本共
元.根据比赛设奖情况,需购买笔记本共![]() 本.
本.
(1)如果购买奖品共花费了![]() 元,这两种笔记本各买了多少本?
元,这两种笔记本各买了多少本?
(2)根据比赛设奖情况,决定所购买的![]() 种笔记本的数量不少于
种笔记本的数量不少于![]() 种笔记本数量,但又不多于
种笔记本数量,但又不多于![]() 种笔记本数量的
种笔记本数量的![]() 倍.设买
倍.设买![]() 种笔记本
种笔记本![]() 本,买两种笔记本的总费为
本,买两种笔记本的总费为![]() 元.
元.
①写出![]() (元)关于
(元)关于![]() (本)的函数关系式,并求出自变量
(本)的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
②购买这两种笔记本各多少本时,花费最少?最少的费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四边形AFOE:S△COD=2:3.
其中正确的结论有_____.(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.
其中说法正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示.已知大棚在地面上的宽度OA为8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的函数关系式;
(2)若借助横梁DE建一个门,要求门的高度不低于1.5米,则横梁DE的宽度最多是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF=![]() AB;G、H分别是BC边上的点,且GH=
AB;G、H分别是BC边上的点,且GH=![]() BC;若S1,S2分别表示EOF和GOH的面积,则S1,S2之间的等量关系是______________
BC;若S1,S2分别表示EOF和GOH的面积,则S1,S2之间的等量关系是______________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com