
【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示.已知大棚在地面上的宽度OA为8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的函数关系式;
(2)若借助横梁DE建一个门,要求门的高度不低于1.5米,则横梁DE的宽度最多是多少米?

科目:初中数学 来源: 题型:
【题目】如图,已△ABC中,AB=AC=12厘米(可得出∠B=∠C),BC=9厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明;
(2)点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,Rt△ABC中,若AC=4,BC=3,DE⊥AC,且DE=DB,求AD的长;
(2)如图2,已知△ABC,若AB边上存在一点M,若AC边上存在一点N,使MB=MN,且△AMN∽△ABC,请利用没有刻度的直尺和圆规,作出符合条件的线段MN(注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注).
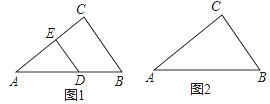
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() (a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )

A. 2a﹣b=0
B. a+b+c>0
C. 3a﹣c=0
D. 当a=![]() 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题
(2x﹣5)2+(3x+7)2=(5x+2)2
解:设m=2x﹣5,n=3x+7,则m+n=5x+2
则原方程可化为m2+n2=(m+n)2
所以mn=0,即(2x﹣5)(3x+7)=0
解之得,x1=![]() ,x2=﹣
,x2=﹣![]()
请利用上述方法解方程(4x﹣5)2+(3x﹣2)2=(x﹣3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二维码已经给我们的生活带来了很大方便,它是由大小相同的黑白两色的小正方形(如图1中C)按某种规律组成的一个大正方形,现有25×25格式的正方形如图1,角上是三个7×7的A型大黑白相间正方形,中间右下一个5×5的B型黑白相间正方形,除这4个正方形外,若其他的小正方形白色块数y与黑色块数x正好满足如图2所示的函数图象,则该25×25格式的二维码共有多少块黑色的C型小正方形( )

A. 153 B. 218 C. 100 D. 216
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com