
分析 由题意可知:①台阶为1阶时,上法有1种;②台阶为2阶时,上法有1+1=2种;③台阶为3阶时,上法有1+2=3种;④台阶为4阶时,上法有2+3=5种;…以此类推得出从台阶数3开始,走法是前两个台阶数上法的总和,由此得出答案即可.
解答 解:①台阶为1阶时,上法有1种;
②台阶为2阶时,上法有1+1=2种;
③台阶为3阶时,上法有1+2=3种;
④台阶为4阶时,上法有2+3=5种;
…
所以上台阶的方法依次有1,2,3,5,8,13,21,34,55,89…;
台阶为10阶时,上法有89种.
故答案为:89.
点评 此题考查图形的变化规律,找出规律解决问题,实际上台阶的上法组成的数列恰好是著名的斐波那数列.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
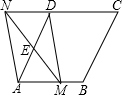 如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
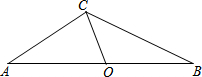 如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,联结BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为20°.
如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,联结BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为20°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 储水池 | 费用(万元/个) | 可供使用户数(户/个) | 占地面积(m2/个) |
| 新建 | 4 | 5 | 4 |
| 维护 | 3 | 18 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com