
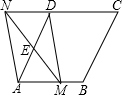
 如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.分析 (1)根据菱形的性质可得AB∥CD,根据两直线平行,内错角相等可得∠NDE=∠MAE,根据对顶角相等可得∠DEN=∠AEM,根据中点的定义求出DE=AE,然后利用“角边角”证明△NDE和△MAE全等,根据全等三角形对应边相等得到ND=AM,然后利用一组对边平行且相等的四边形是平行四边形证明;
(2)首先证明△AEM是等边三角形,进而得到AE=ED=EM,利用三角形一边上的中线等于斜边一半判断出△AMD是直角三角形,进而得出四边形AMDN是矩形.
解答 解:(1)∵点E是AD边的中点,
∴AE=ED,
∵AB∥CD,
∴∠NDE=∠MAE,
在△NDE和△MAE中,
$\left\{\begin{array}{l}{∠NDE=∠MAE}\\{DE=AE}\\{∠NED=∠MEA}\end{array}\right.$,
∴△NDE≌△MAE(ASA),
∴ND=AM,
∵ND∥AM,
∴四边形AMDN是平行四边形;
(2)当AM=2时,说明四边形是矩形.
∵E是AD的中点,
∴AE=2,
∵AE=AM,∠EAM=60°,
∴△AME是等边三角形,
∴AE=EM,
∴AE=ED=EM,
∴∠AMD=90°,
∵四边形ABCD是菱形,
故当AM=2时,四边形AMDN是矩形.
点评 本题考查了菱形的性质,平行四边形的判定,全等三角形的判定与性质,矩形的性质,熟记各性质并求出三角形全等是解题的关键,也是本题的突破口.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 根据图示,回答下列问题
根据图示,回答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
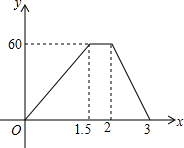 一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.
一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6个只有颜色不同的小球 | |
| B. | 两个骰子 | |
| C. | 三个硬币 | |
| D. | 只有颜色不同的小卡片6张,其中红、白、黄各占2张 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com