练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．6名学生中，初一、初二、初三各占2名，若从这6名学生中任意选取3名，实验估计选取的3名学生中，两两不在同一年段的概率，那么下列实物可以直接作为模拟实验中的替代物的是（　　）
    A．6个只有颜色不同的小球
    B．两个骰子
    C．三个硬币
    D．只有颜色不同的小卡片6张，其中红、白、黄各占2张

    分析 模拟实验中的替代物能表示不同三个年级，也能表示6个学生，于是可判断D正确．

    解答 解：模拟实验中的替代物要能代表初一、初二、初三各2名的学生，而6个只有颜色不同的小球不能区分年级，两个骰子和三个硬币不能代表6名学生，只有颜色不同的小卡片6张可代表6名学生，其中红、白、黄代表三个不同年级．
    故选D．

    点评 本题考查了模拟实验：在一些有关抽取实物实验中通常用摸取卡片代替了实际的物品或人抽取，这样的实验称为模拟实验．模拟实验是用卡片、小球编号等形式代替实物进行实验，或用计算机编号等进行实验，目的在于省时、省力，但能达到同样的效果．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．如图所示，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足$\frac{CF}{FD}$=$\frac{1}{3}$，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．给出下列结论：
    ①△ADF∽△AED；②FG=2；③DC平分∠ADE；④CG2=AG•BG；
    其中结论正确的是（　　）
    A．①②B．①②③C．①②④D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

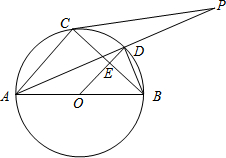    16．如图，⊙O是以AB为直径的△ABC的外接圆，点D是劣弧$\widehat{BC}$的中点，连结AD并延长，与过C点的直线交于P，OD与BC相交于点E．
    （1）求证：OE=$\frac{1}{2}$AC；
    （2）连接CD，若∠PCD=∠PAC，试判断直线PC与⊙O的位置关系，并说明理由．
    （3）在（2）的条件下，当AC=6，AB=10时，求切线PC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

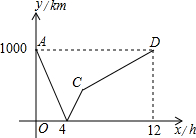    13．如图所示，一列快车从甲地开往乙地，一列慢车从乙地开往甲地，两车同时出发，设慢车行驶的时间为x小时，两车之间的距离为y千米，图中的折线表示y与x之间的函数关系，则快车的速度是$166\frac{2}{3}$千米/小时．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

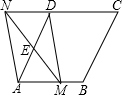    20．如图，在菱形ABCD中，AB=4，∠DAB=60°，点E是AD边的中点，点M是AB边上的一个动点（不与点A重合），延长ME交CD的延长线于点N，连接MD，AN．
    （1）求证：四边形AMDN是平行四边形；
    （2）当AM的值为2时，四边形AMDN是矩形，请你把猜想出的AM值作为已知条件，说明四边形AMDN是矩形的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

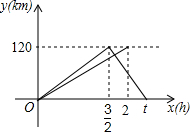    10．一辆轿车从甲地驶往乙地，到达乙地后立即返回甲地，速度是原来的1.5倍，往返共用t小时；一辆货车同时从甲地驶往乙地，到达乙地后停止，两车同时出发，匀速行驶，设轿车行驶的时间为x（h），两车离开甲地的距离为y（km），两车行驶过程中y与x之间的函数图象如图所示．
    （1）轿车从乙地返回甲地的速度为120km/h，t=$\frac{5}{2}$；
    （2）求轿车从乙地返回甲地时y与x之间的函数关系式；
    （3）当轿车从甲地返回乙地的途中与货车相遇时，求相遇处到甲地的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

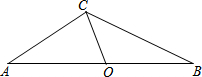    17．如图，已知钝角三角形ABC，∠A=35°，OC为边AB上的中线，将△AOC绕着点O顺时针旋转，点C落在BC边上的点C′处，点A落在点A′处，联结BA′，如果点A、C、A′在同一直线上，那么∠BA′C′的度数为20°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．某村为了确保村民生活生产用水，春季准备由村委会和村民共同集资新建储水池和维护原有储水池共20个．费用和可供使用的户数及占地情况如下表：
    储水池费用（万元/个）可供使用户数（户/个）占地面积（m2/个）
    新建454
    维护3186
    已知：可使用的土地面积109m，村民共有243户．
    请解答下列问题：
    （1）有几种实施方案？
    （2）若每户村民平均集资0.2万元，村委会最少出资多少钱？
    （3）在（2）的条件下，由甲、乙两个施工队共同承包此项工程，已知甲施工队新建一个储水池和维护两个储水池，恰好用7天；乙施工队新建一个储水池和维护4个储水池恰好用12天．直接写出甲、乙两队各施工多少天？（两施工队的工作天数都是整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

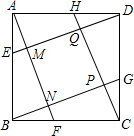    15．已知，如图，在正方形ABCD的各边上截取AE=BF=CG=DH，连接AF、BG、CH、DE，依次相交于点N、P、Q、M，求证：四边形MNPQ是正方形．

    查看答案和解析>>

    同步练习册答案