
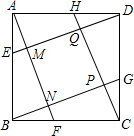
 已知,如图,在正方形ABCD的各边上截取AE=BF=CG=DH,连接AF、BG、CH、DE,依次相交于点N、P、Q、M,求证:四边形MNPQ是正方形.
已知,如图,在正方形ABCD的各边上截取AE=BF=CG=DH,连接AF、BG、CH、DE,依次相交于点N、P、Q、M,求证:四边形MNPQ是正方形. 分析 先证明三角形全等,得出对应角相等,根据角的互余关系得出四边形MNPQ的三个角是直角,则四边形是矩形,然后证明三角形全等得出一组邻边相等,可以证得四边形是正方形.
解答 证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAD=∠ABC=∠BCD=∠CDA=90°,
在△ABF和△BCG中,
$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠ABC=∠BCD}&{\;}\\{BF=CG}&{\;}\end{array}\right.$,
∴△ABF≌△BCG(SAS)
∴∠BAF=∠GBC,
∵∠BAF+∠AFB=90°,
∴∠GBC+∠AFB=90°,
∴∠BNF=90°,
∴∠MNP=90°.
∴同理可得∠NPQ=∠PQM=90°,
∴四边形MNPQ是矩形.
在△ABN和△BCP中,
$\left\{\begin{array}{l}{∠BAF=∠GBC}&{\;}\\{∠ANB=∠BPC}&{\;}\\{AB=BC}&{\;}\end{array}\right.$,
∴△ABN≌△BCP(AAS),
∴AN=BP,
在△AME和△BNF中,
$\left\{\begin{array}{l}{∠BAF=∠GBC}&{\;}\\{∠AME=∩BNF}&{\;}\\{AE=BF}&{\;}\end{array}\right.$,
∴△AME≌△BNF(AAS),
∴AM=BN,
∴MN=NP,
∴矩形MNPQ是正方形.
点评 本题考查了正方形的判定与性质、全等三角形判定与性质、矩形的判定;证明三角形全等是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 6个只有颜色不同的小球 | |
| B. | 两个骰子 | |
| C. | 三个硬币 | |
| D. | 只有颜色不同的小卡片6张,其中红、白、黄各占2张 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
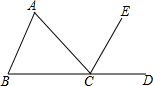 如图,点B、C、D在同一直线上,∠A=∠B.
如图,点B、C、D在同一直线上,∠A=∠B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com