
分析 先设二次函数的解析式为y=a(x-h)2+k,再把顶点坐标为(-3,$\frac{1}{2}$),点(2,$\frac{11}{2}$)代入即可得出二次函数的解析式,然后令x=0,即可得出该函数图象与y轴的交点坐标.
解答 解:设二次函数的解析式为y=a(x-h)2+k,
把h=-3,k=$\frac{1}{2}$,和点(2,$\frac{11}{2}$)代入y=a(x-h)2+k,得a(2+3)2+$\frac{1}{2}$=$\frac{11}{2}$,
解得a=$\frac{1}{5}$,
所以二次函数的解析式为y=$\frac{1}{5}$(x+3)2+$\frac{1}{2}$,
当x=0时,y=$\frac{1}{5}$×9+$\frac{1}{2}$=$\frac{23}{10}$,
所以函数图象与y轴的交点坐标(0,$\frac{23}{10}$).
点评 本题考查了用待定系数法求二次函数的解析式和其顶点坐标、抛物线与x轴y轴的交点坐标的求法.解题的关键是:设二次函数的解析式为y=a(x-h)2+k.


科目:初中数学 来源: 题型:填空题
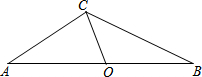 如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,联结BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为20°.
如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,联结BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为20°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
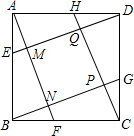 已知,如图,在正方形ABCD的各边上截取AE=BF=CG=DH,连接AF、BG、CH、DE,依次相交于点N、P、Q、M,求证:四边形MNPQ是正方形.
已知,如图,在正方形ABCD的各边上截取AE=BF=CG=DH,连接AF、BG、CH、DE,依次相交于点N、P、Q、M,求证:四边形MNPQ是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com