
 如图,∠BAD=∠CBE=∠ACF,∠FDE=64°,∠DEF=43°,求△ABC各内角的度数.
如图,∠BAD=∠CBE=∠ACF,∠FDE=64°,∠DEF=43°,求△ABC各内角的度数. 分析 根据三角形外角性质得到∠FDE=∠BAD+∠ABD,而∠BAD=∠CBE,则∠FDE=∠BAD+∠CBE=∠ABC=64°;同理可得∠DEF=∠ACB=43°,然后根据三角形内角定理计算∠BAC=180°-∠ABC-∠ACB即可.∠BAD=∠CBE=∠ACF,∠FDE=48°,∠DEF=64°,
解答 解:∵∠FDE=∠BAD+∠ABD,∠BAD=∠CBE
∴∠FDE=∠BAD+∠CBE=∠ABC,
∴∠ABC=64°;
同理∠DEF=∠FCB+∠CBE=∠FCB+∠ACF=∠ACB,
∴∠ACB=43°;
∴∠BAC=180°-∠ABC-∠ACB=180°-64°-43°=73°,
∴△ABC各内角的度数分别为64°、43°、73°.
点评 本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形外角的性质,熟记:三角形的外角等于与它不相邻的两个内角之和是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
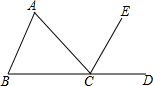 如图,点B、C、D在同一直线上,∠A=∠B.
如图,点B、C、D在同一直线上,∠A=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
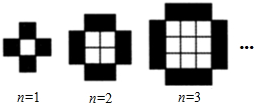 当白色小正方形个数n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形的个数是n2和黑色小正方形的个数是4n(用n表示,n是正整数).
当白色小正方形个数n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形的个数是n2和黑色小正方形的个数是4n(用n表示,n是正整数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com