
分析 (1)根据根与系数的关系和倒数的定义得到关于m的方程,通过解该方程来求m的值;
(2)根据根与系数的关系和相反数的定义得到关于m的方程,通过解该方程来求m的值;
(3)把x=1代入已知方程,列出关于m的新方程,通过解新方程来求m的值.
解答 解:△=16(m-1)2-4(1-m2)×(-4)=32-32m≥0,解得m≤1.
(1)依题意得 $\frac{-4}{1-{m}^{2}}$=1,
整理,得m2=5,
解得 m1=1+$\sqrt{5}$(舍去),m2=1-$\sqrt{5}$;
.
(2)依题意得-$\frac{-4(m-1)}{1-{m}^{2}}$=0,
则m-1=0,
解得 m=1.
(3)把x=1代入(1-m2)x2-4(m-1)x-4=0,得
(1-m2)-4(m-1)-4=0,
整理得:m2+4m-1=0,
则m=$\frac{-4±\sqrt{16+4}}{2}$=-2±$\sqrt{5}$,
解得 m1=-2+$\sqrt{5}$(舍去),m2=-2-$\sqrt{5}$.
点评 本题考查了根与系数的关系和根的判别式.注意,一定要根据根的判别式来求得m的取值范围,然后根据所求的m的值进行取舍.


科目:初中数学 来源: 题型:解答题
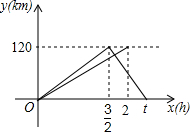 一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止,两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.
一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止,两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
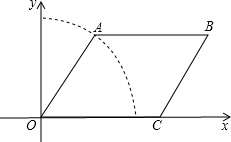 如图,点A是以O为圆心的圆上的一个动点,点C是x轴正半轴上的一个动点,BC∥OA,AB∥x轴.
如图,点A是以O为圆心的圆上的一个动点,点C是x轴正半轴上的一个动点,BC∥OA,AB∥x轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
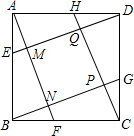 已知,如图,在正方形ABCD的各边上截取AE=BF=CG=DH,连接AF、BG、CH、DE,依次相交于点N、P、Q、M,求证:四边形MNPQ是正方形.
已知,如图,在正方形ABCD的各边上截取AE=BF=CG=DH,连接AF、BG、CH、DE,依次相交于点N、P、Q、M,求证:四边形MNPQ是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
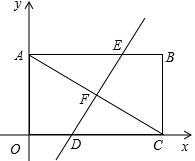 如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.
如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com